Photo AI
Here is Mario's answer to a question - OCR - GCSE Maths - Question 3 - 2018 - Paper 4
Question 3
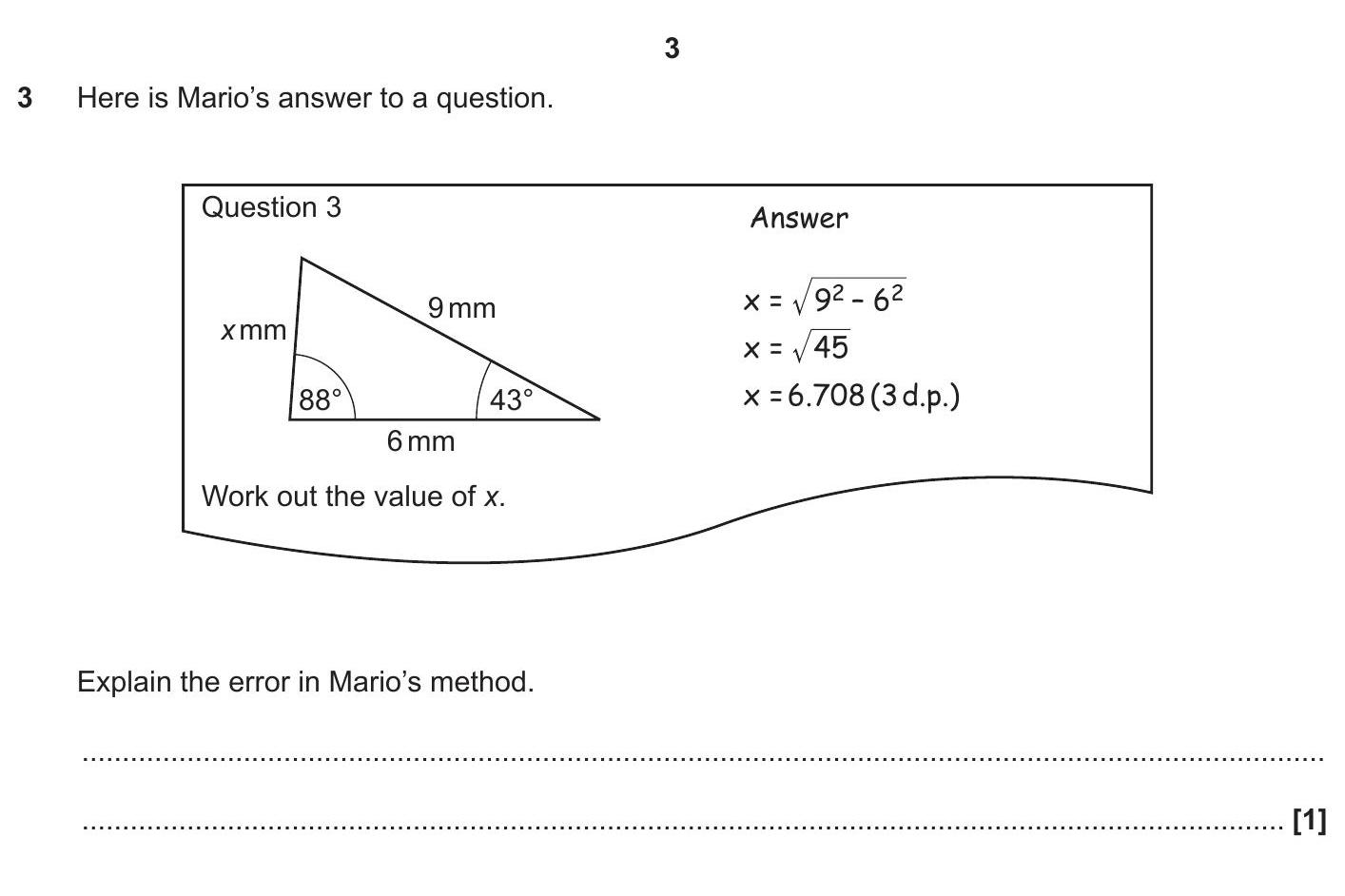
Here is Mario's answer to a question. Question 3 ``` x mm /| / | 9 mm / | / | / | 88° / | ------- 6 mm 43° ``` Work out the v... show full transcript
Worked Solution & Example Answer:Here is Mario's answer to a question - OCR - GCSE Maths - Question 3 - 2018 - Paper 4
Step 1
Step 2
Explain the error in Mario's method.
Answer
Mario's method is incorrect because he assumed that the triangle is a right-angled triangle. However, this triangle is not right-angled, as indicated by the angles provided (88° and 43°). Therefore, he should not use the Pythagorean theorem () for his calculations. Instead, he should have applied either the sine rule or the cosine rule to find the correct value of .
