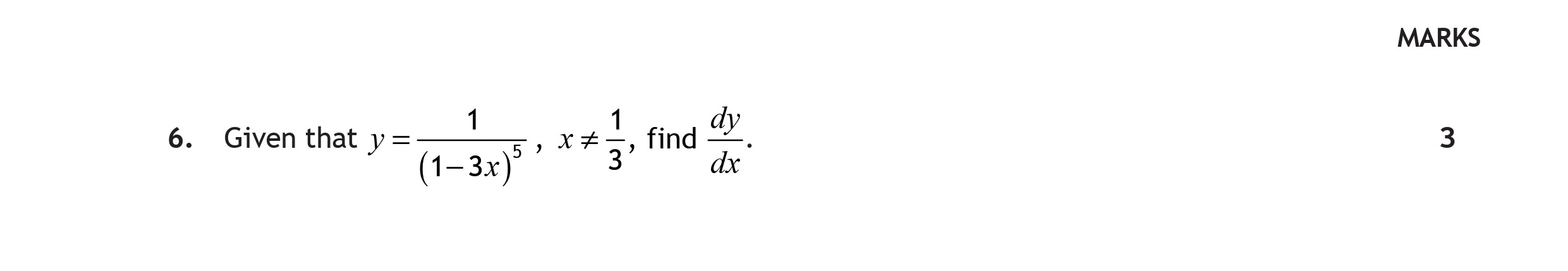Given that
y = \frac{1}{(1-3x)^{3}} x^{\frac{1}{3}} find \frac{dy}{dx}. - Scottish Highers Maths - Question 6 - 2019

Question 6
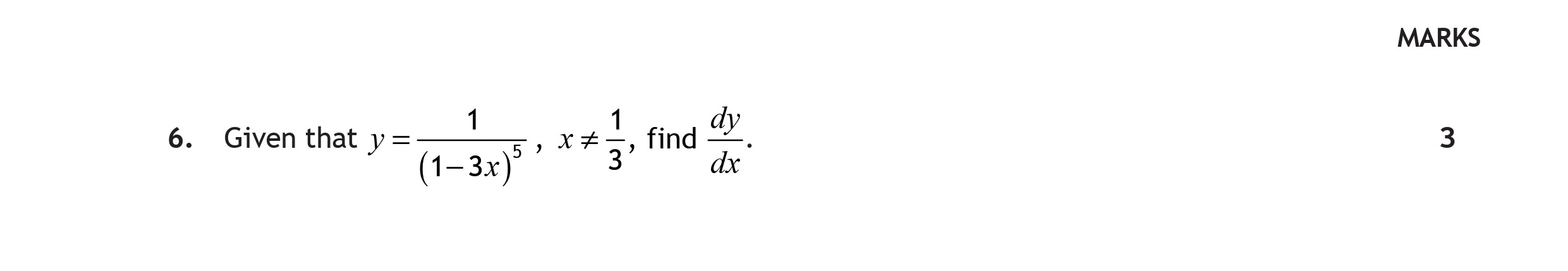
Given that
y = \frac{1}{(1-3x)^{3}} x^{\frac{1}{3}} find \frac{dy}{dx}.
Worked Solution & Example Answer:Given that
y = \frac{1}{(1-3x)^{3}} x^{\frac{1}{3}} find \frac{dy}{dx}. - Scottish Highers Maths - Question 6 - 2019
Rewrite in differentiable form

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
To differentiate the function, we rewrite it in a more manageable form:
y=(1−3x)−3x1/3
Start to differentiate

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
We will apply the product rule for differentiation. Let:
- u = (1−3x)−3
- v = x1/3
The product rule states that:
dxdy=dxduv+udxdv
Complete differentiation

Only available for registered users.
Sign up now to view full answer, or log in if you already have an account!
Now, we differentiate u and v:
-
For u=(1−3x)−3:
dxdu=−3(1−3x)−4(−3)=9(1−3x)−4
-
For v=x1/3:
dxdv=31x−2/3
Now substituting these back into the product rule:
dxdy=9(1−3x)−4⋅x1/3+(1−3x)−3⋅31x−2/3
This simplifies to:
dxdy=9x1/3(1−3x)−4+31(1−3x)−3x−2/3
Join the Scottish Highers students using SimpleStudy...
97% of StudentsReport Improved Results
98% of StudentsRecommend to friends
100,000+ Students Supported
1 Million+ Questions answered