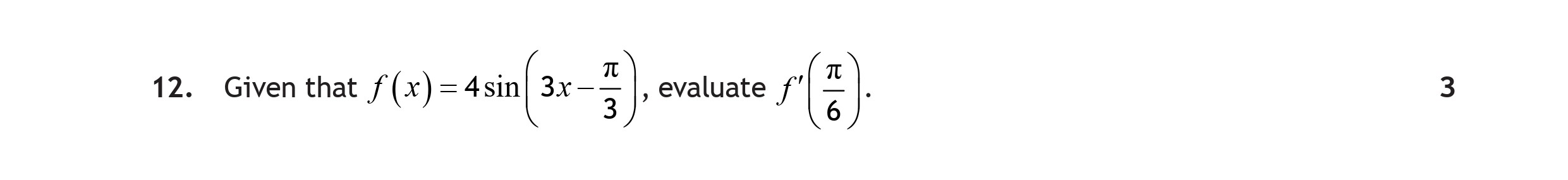Photo AI

Given that $f(x) = 4 \sin\left( 3x - \dfrac{\pi}{3} \right)$ evaluate $f\left( \dfrac{\pi}{6} \right)$. - Scottish Highers Maths - Question 12 - 2022

Question icon

Question 12

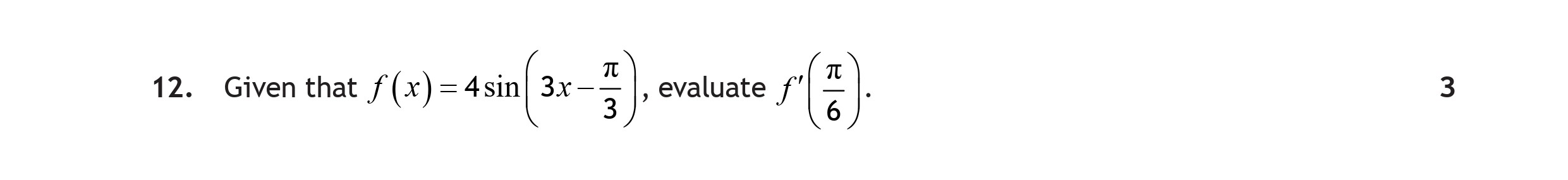
Given-that-$f(x)-=-4-\sin\left(-3x---\dfrac{\pi}{3}-\right)$-evaluate-$f\left(-\dfrac{\pi}{6}-\right)$.-Scottish Highers Maths-Question 12-2022.png

Given that $f(x) = 4 \sin\left( 3x - \dfrac{\pi}{3} \right)$ evaluate $f\left( \dfrac{\pi}{6} \right)$.

Worked Solution & Example Answer:Given that $f(x) = 4 \sin\left( 3x - \dfrac{\pi}{3} \right)$ evaluate $f\left( \dfrac{\pi}{6} \right)$. - Scottish Highers Maths - Question 12 - 2022

Step 1

Differentiate $f(x)$

96%

114 rated

Answer

To differentiate the function, we use the chain rule. The derivative of sin⁡(u)\sin(u) is cos⁡(u)\cos(u) multiplied by the derivative of uu. Here, let u=3x−π3u = 3x - \dfrac{\pi}{3}, thus:

f′(x)=4cos⁡(3x−π3)⋅ ddx(3x−π3)=4cos⁡(3x−π3)⋅3=12cos⁡(3x−π3).f'(x) = 4 \cos(3x - \dfrac{\pi}{3}) \cdot \,\frac{d}{dx}(3x - \dfrac{\pi}{3}) = 4 \cos(3x - \dfrac{\pi}{3}) \cdot 3 = 12 \cos(3x - \dfrac{\pi}{3}).

Step 2

Evaluate $f'\left( \dfrac{\pi}{6} \right)$

99%

104 rated

Answer

Substituting x=π6x = \dfrac{\pi}{6} into the derivative:

f′(π6)=12cos⁡(3⋅π6−π3).f'\left( \dfrac{\pi}{6} \right) = 12 \cos\left( 3 \cdot \dfrac{\pi}{6} - \dfrac{\pi}{3} \right).

Calculating the argument of the cosine:

3⋅π6=π2thus,π2−π3=3π−2π6=π6.3 \cdot \dfrac{\pi}{6} = \dfrac{\pi}{2}\quad \text{thus,}\quad \dfrac{\pi}{2} - \dfrac{\pi}{3} = \dfrac{3\pi - 2\pi}{6} = \dfrac{\pi}{6}.

Now, we evaluate:

f′(π6)=12cos⁡(π6)=12⋅32=63.f'\left( \dfrac{\pi}{6} \right) = 12 \cos\left( \dfrac{\pi}{6} \right) = 12 \cdot \dfrac{\sqrt{3}}{2} = 6\sqrt{3}.

Join the Scottish Highers students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;