2.2.1 Using Calculus in 1D

Variable Acceleration

The motion of an object can be modelled by using formulas given in terms of time.

e.g., $x = t^3 - 6t + 8$ can be used to model the position x of a particle at time t seconds.

Sketching this curve

Roots: t = 4, 2 (from calculator)
Intercept: 8
Minimum point: t = 3, x = -1 $\text{Min point: } t = 3 \Rightarrow x = 3^3 - 6(3) + 8 = -1$

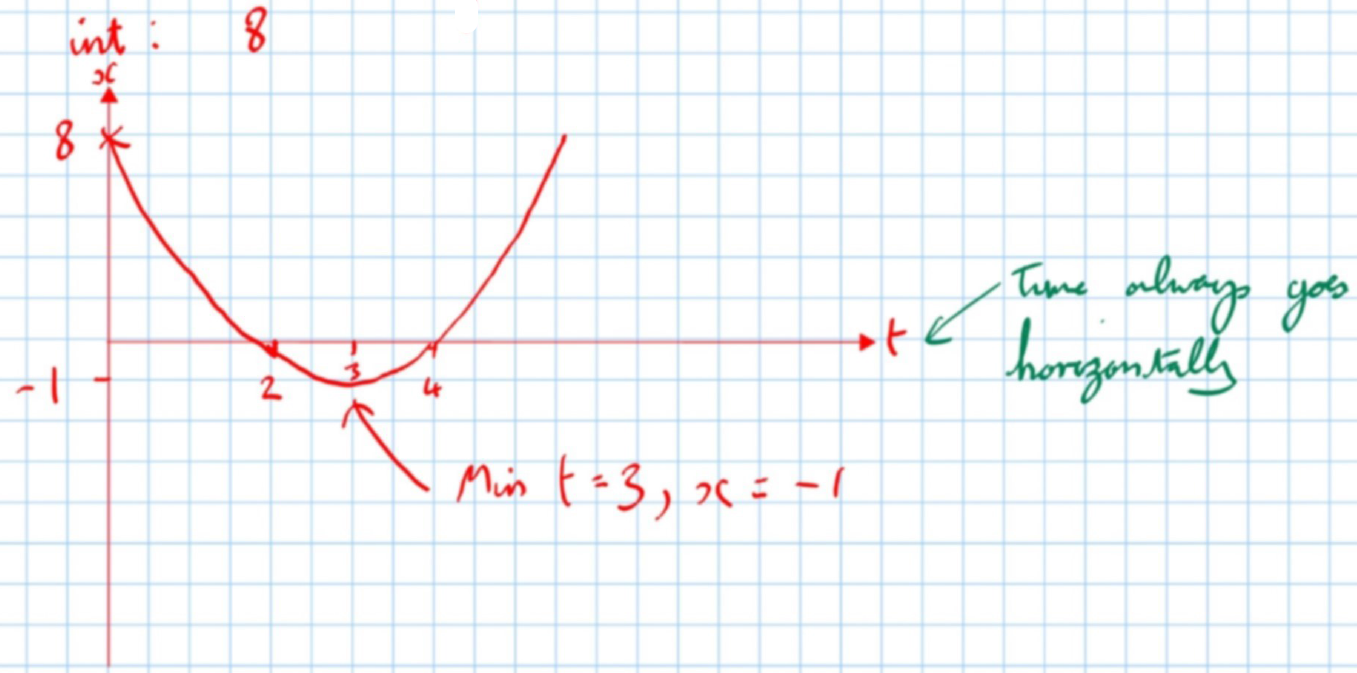
In this situation, the turning point of the particle is the point at which the particle has no speed, i.e., the particle is stationary.

Terminology

Displacement: How far a particle is from the origin where negative and positive directions matter.
Distance: How far something has travelled relative to an origin.

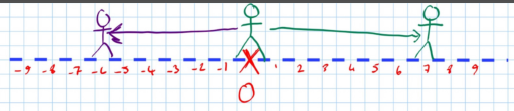
In this situation, the person walks a distance of 7 m, displacing himself 7 m from the origin.

In this example, he walks a distance of 6m, displacing himself 6m from the origin.

Definitions:

infoNote

Velocity: Rate of change of displacement (direction matters).
Speed: Rate of change of distance (direction doesn't matter).

Differentiation and Integration:

infoNote

\frac{d}{dt} s = \text{displacement} \quad \Rightarrow \quad \int dt

v = \frac{ds}{dt} = \text{velocity} \quad \Rightarrow \quad \int dt

a = \frac{dv}{dt} = \frac{d^2 s}{dt^2} = \text{acceleration}

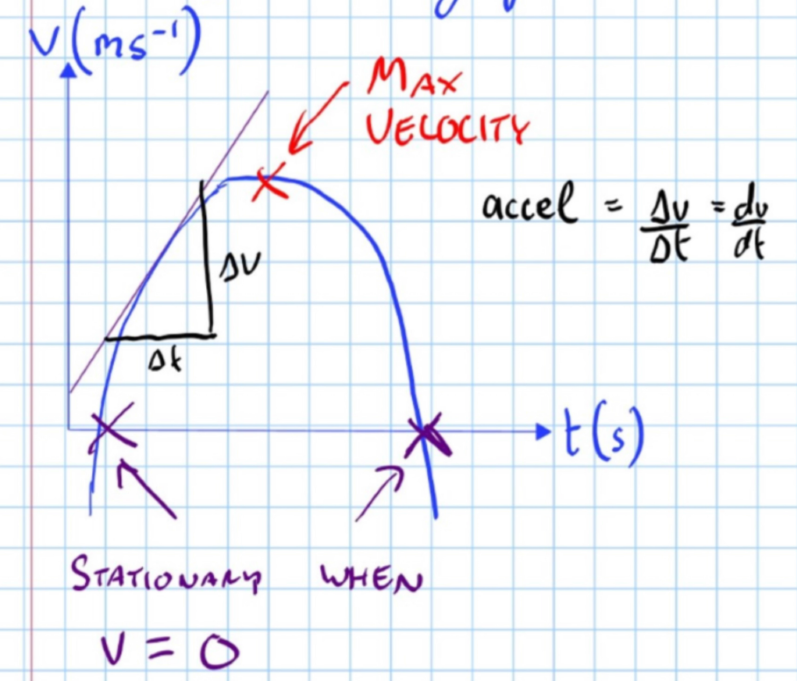
Velocity-Time Graph $(v-t)$ :

Max Velocity
Acceleration: $\text{accel} = \frac{\Delta v}{\Delta t} = \frac{dv}{dt}$
Stationary when v = 0

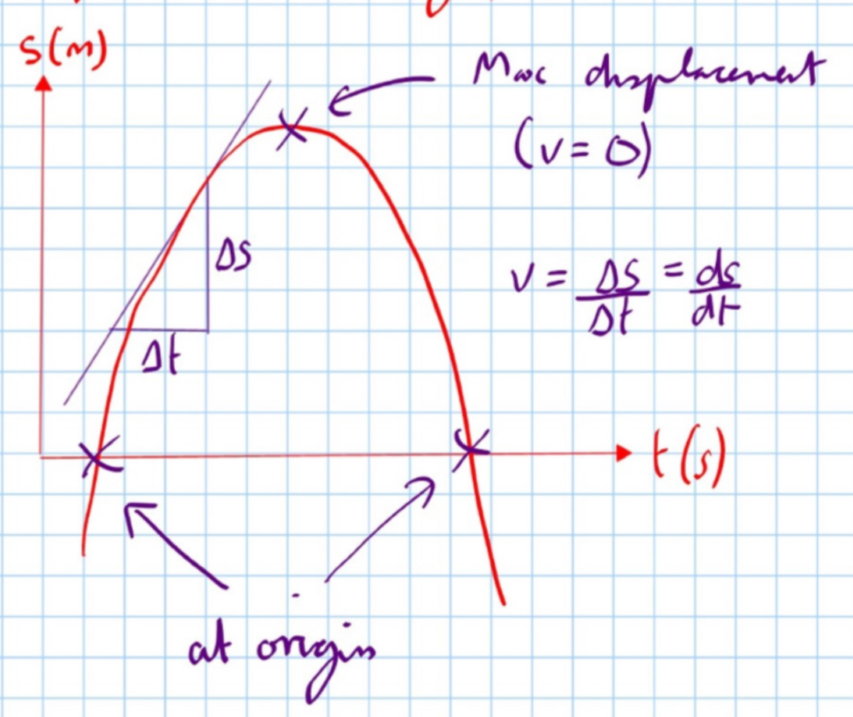
Displacement-Time Graph ( $s-t$ ):

Max displacement (when v = 0)
$\Delta s over \Delta t$
$v = \frac{\Delta s}{\Delta t} = \frac{ds}{dt}$
At origin

infoNote

Example: A particle is travelling with the trajectory $s = t^2 + 6t - 4$ .

Find its velocity in terms of t and therefore its minimum displacement.
Comment on the acceleration of the particle. a) The velocity $v$ is given by:

v = \frac{ds}{dt} = 2t + 6

At minimum displacement, ds/dt = 0:

2t + 6 = 0 \quad \Rightarrow \quad 2t = -6 \quad \Rightarrow \quad t = -3\ When\ t = -3:

s = (-3)^2 + 6(-3) - 4 = 9 - 18 - 4 = \mathbf{-13 \text{ m}}

(Negative time $t$ indicates the time before the reference point.)

b) The acceleration a is given by:

a = \frac{dv}{dt} = 2

Acceleration is positive and constant, which means the particle will get faster and faster.

infoNote

A particle $P$ moves in a straight line such that its distance, s meters, from a fixed point $O$ at time $t$ is given by:

s = 0.4t^3 - 0.3t^2 - 1.8t + 5, \quad 0 \leq t \leq 3

The diagram shows the displacement-time graph of the motion of $P$ .

a) Determine the time at which $P$ is moving with minimum velocity.

b) Find the displacement of $P$ from $O$ at this time.

c) Find the velocity of $P$ at this time.

Solution:

s = 0.4t^3 - 0.3t^2 - 1.8t + 5

v = \frac{ds}{dt} = 1.2t^2 - 0.6t - 1.8

\frac{dv}{dt} = 2.4t - 0.6 = 0

Velocity is at maximum or minimum when dv/dt = 0:

2.4t - 0.6 = 0 \Rightarrow t = \frac{0.6}{2.4} = \mathbf{\frac{1}{4} \text{ seconds}}

b) Let $t = 0.25$ :

s = 0.4(0.25)^3 - 0.3(0.25)^2 - 1.8(0.25) + 5 = \mathbf{4.5375 \text{ m}}

c) Let $t = 0.25$ :

v = 1.2(0.25)^2 - 0.6(0.25) - 1.8 = \mathbf{-1.2375 \text{ ms}^{-1}}

Integration in Variable Acceleration Problems

infoNote

Example: Given that $V = 4t^2 - t^3$ and that initially a particle is at the origin, find the total displacement in the first 8 seconds of motion of the particle.

Method 1: Differential Equations

\frac{ds}{dt} = 4t^2 - t^3 \Rightarrow s = \int (4t^2 - t^3) \, dt

s = \frac{4t^3}{3} - \frac{t^4}{4} + c

Using the initial condition:

\text{Let } t = 0, \, s = 0 \Rightarrow 0 = \frac{4(0)^3}{3} - \frac{0^4}{4} + c \Rightarrow c = 0

\therefore s = \frac{4t^3}{3} - \frac{t^4}{4}

For $t = 8$ :

s = \frac{4(8)^3}{3} - \frac{8^4}{4} = \mathbf{-\frac{1024}{3} \, \text{m}}

Method 2: Integration with Limits

s = \int_0^8 (4t^2 - t^3) \, dt

Using the calculator:

\int_0^8 (4x^2 - x^3) \, dx = \mathbf{-\frac{1024}{3}}

infoNote

Q4 (Jan 2011, Q6) The velocity $v \, \text{ms}^{-1}$ of a particle at time t is given by $v = t^2 - 9$ . The particle travels in a straight line and passes through a fixed point $O$ when $t = 2. (t, s) = (2, 0)$

(i) Find the displacement of the particle from O when $t = 0.$
(ii) Calculate the distance the particle travels from its position at $t = 0$ until it changes its direction of motion.
(iii) Calculate the distance of the particle from O when the acceleration of the particle is $10 \, \text{ms}^{-2}.$

Solution:

(i)

v = t^2 - 9 \Rightarrow \text{c} = \int (t^2 - 9) \, dt = \frac{1}{3} t^3 - 9t + c

Let $(t, s) = (2, 0)$ :

0 = \frac{1}{3} (2)^3 - 9(2) + c \Rightarrow c = 9(2) - \frac{1}{3} (2)^3

s = \frac{1}{3} t^3 - 9t + \frac{46}{3}

When $t = 0$ , $s = \mathbf{\frac{46}{3}}$ .

(ii) Note: When a particle changes direction, v = 0.

v = t^2 - 9 = 0 \Rightarrow t^2 = 9 \Rightarrow t = 3

For $t = 3$ , $s = \frac{1}{3}(3)^3 - 9(3) + \frac{46}{3} = -\frac{8}{3}$ .

t = 0 \Rightarrow s = \frac{46}{3}

Distance from start:

\frac{46}{3} - \left(-\frac{8}{3}\right) = \mathbf{18}

(iii)

\frac{dv}{dt} = 2t = 10 \Rightarrow t = 5

When $t = 5$ :

s = \frac{1}{3} (5)^3 - 9(5) + \frac{46}{3} = \mathbf{12}

infoNote

Q5 (Jun 2014, Q3) A particle $P$ travels in a straight line. The velocity of $P$ at time $t$ seconds after it passes through a fixed point $A$ is given by $(0.6t^2 + 3) \, \text{ms}^{-1}$ . Find

(i) the velocity of P when it passes through A.
(ii) the displacement of P from A when t = 1.5.
(iii) the velocity of P when it has acceleration $6 \, \text{ms}^{-2}$ .

Solution:

(i)

v = 0.6t^2 + 3 \Rightarrow \text{at} \, t = 0, \, v = \mathbf{3 \, \text{ms}^{-1}}

(ii)

s = \int (0.6t^2 + 3) \, dt \Rightarrow s = \frac{0.6t^3}{3} + 3t + c

At $t = 0, \, s = 0$ :

0 = 0 + c \Rightarrow c = 0

S = 0.2t^3 + 3t \Rightarrow \text{at} \, t = 1.5, \, s = 0.2(1.5)^3 + 3(1.5) = \mathbf{5.175 \, \text{m}}

(iii)

\frac{dv}{dt} = 1.2t = 6 \Rightarrow t = 5

v = 0.6(5)^2 + 3 = \mathbf{18 \, \text{ms}^{-1}}

infoNote

Q8. (OCR 4761, Jan 2008, Q5)

A toy car is moving along the straight line Ox, where O is the origin. The time t is in seconds. At time $t = 0$ the car is at A, 3 m from O as shown in Fig. 5. The velocity of the car, $v \, \text{ms}^{-1}$ , is given by

v = 2 + 12t - 3t^2

Calculate the distance of the car from O when its acceleration is zero.

Solution:

Integrate velocity to find displacement:

s = \int (2 + 12t - 3t^2) \, dt = 2t + 6t^2 - t^3 + c

At $t = 0, s = 3$ :

3 = 2(0) + 6(0)^2 - (0)^3 + c

\Rightarrow c = 3

So,

s = 2t + 6t^2 - t^3 + 3

Find acceleration by differentiating velocity:

a = \frac{dv}{dt} = 12 - 6t

Set acceleration to zero and solve for $t$ :

12 - 6t = 0 \Rightarrow 12 = 6t \Rightarrow t = 2

Substitute $t = 2$ into the displacement equation:

s = 2(2) + 6(2)^2 - (2)^3 + 3 = \mathbf{23 \, \text{m}}

Using Calculus in 1D Simplified Revision Notes for A-Level AQA Maths Mechanics

2.2.1 Using Calculus in 1D

Variable Acceleration

Sketching this curve

Terminology

Definitions:

Differentiation and Integration:

Velocity-Time Graph $(v-t)$ :

Displacement-Time Graph ( $s-t$ ):

Solution:

Integration in Variable Acceleration Problems

Example: Given that $V = 4t^2 - t^3$ and that initially a particle is at the origin, find the total displacement in the first 8 seconds of motion of the particle.

Method 1: Differential Equations

Method 2: Integration with Limits

500K+ Students Use These Powerful Tools to Master Using Calculus in 1D For their A-Level Exams.

Other Revision Notes related to Using Calculus in 1D you should explore

Using Calculus in 1D Simplified Revision Notes for A-Level AQA Maths Mechanics

2.2.1 Using Calculus in 1D

Variable Acceleration

Sketching this curve

Terminology

Definitions:

Differentiation and Integration:

Velocity-Time Graph (v−t)(v-t)(v−t):

Displacement-Time Graph (s−ts-ts−t):

Solution:

Integration in Variable Acceleration Problems

Example: Given that V=4t2−t3V = 4t^2 - t^3V=4t2−t3 and that initially a particle is at the origin, find the total displacement in the first 8 seconds of motion of the particle.

Method 1: Differential Equations

Method 2: Integration with Limits

500K+ Students Use These Powerful Tools to Master Using Calculus in 1D For their A-Level Exams.

Other Revision Notes related to Using Calculus in 1D you should explore

Velocity-Time Graph $(v-t)$ :

Displacement-Time Graph ( $s-t$ ):

Example: Given that $V = 4t^2 - t^3$ and that initially a particle is at the origin, find the total displacement in the first 8 seconds of motion of the particle.