Photo AI
Last Updated Sep 26, 2025
Coefficient of Friction - Inclined Planes Simplified Revision Notes for A-Level AQA Maths Mechanics
Revision notes with simplified explanations to understand Coefficient of Friction - Inclined Planes quickly and effectively.
303+ students studying
3.3.4 Coefficient of Friction - Inclined Planes
When dealing with inclined planes in mechanics, the coefficient of friction plays a crucial role in determining whether an object will slide down the slope or remain stationary. Let's break this down step by step.
Understanding the Scenario
Imagine you have a block resting on a slope (an inclined plane). The slope makes an angle with the horizontal. There are two main forces acting on the block:
- Gravitational Force : Acts vertically downward.
- Normal Force : Acts perpendicular to the surface of the slope, pushing the block upwards.
Resolving the Forces
The gravitational force can be resolved into two components:
- Component parallel to the slope: (this force tries to slide the block down the slope).
- Component perpendicular to the slope: (this force is balanced by the normal force
Frictional Force
The frictional force opposes the motion of the block sliding down the slope. The maximum value of this frictional force is given by:
where is the coefficient of friction, and is the normal force.
Normal Force
Since the normal force is balancing the perpendicular component of the gravitational force:
Condition for Motion
The block will start to slide down the plane if the parallel component of the gravitational force exceeds the maximum frictional force . So, the condition for the block to just start moving is:
Substituting , we get:
Cancelling from both sides:
Summary
- Coefficient of Friction : This determines how much frictional force is available to oppose motion. On an inclined plane, if the object is just about to slide.
- Key Forces: The weight of the object is split into components parallel and perpendicular to the slope, influencing the friction and normal force.
- Critical Angle: The angle where the object starts to slide is directly related to . If increases beyond a certain point, the object will start to slide down the plane.
Example Problem
Problem: A block of mass kg is resting on an inclined plane that makes an angle of ° with the horizontal. If the coefficient of friction between the block and the plane is ,
Question : will the block slide down the plane?
Solution:
- Calculate the forces:
- Parallel force:
- Normal force:
- Calculate the maximum frictional force:
- Compare the forces:
- The parallel force () is greater than the maximum frictional force (), so the block will slide down the plane. This example shows how the balance between gravitational and frictional forces determines whether an object will slide down an inclined plane.
Example: Force on a Slope with Friction
Problem Statement:
-
A box of mass kg is held in limiting equilibrium on a slope inclined at by a force .
-
The coefficient of friction between the block and the plane is . Question
-
Find the value of if the block is:
- On the point of moving down the slope.
- On the point of moving up the slope.
Part (a): On the Point of Moving Down the Slope
- Forces acting:
- Gravitational force component along the slope:
- Normal reaction force:
- Frictional force:
- Force acting up the slope.
- Equations of equilibrium:
- For vertical equilibrium:
- For horizontal equilibrium (resolving forces along the slope):
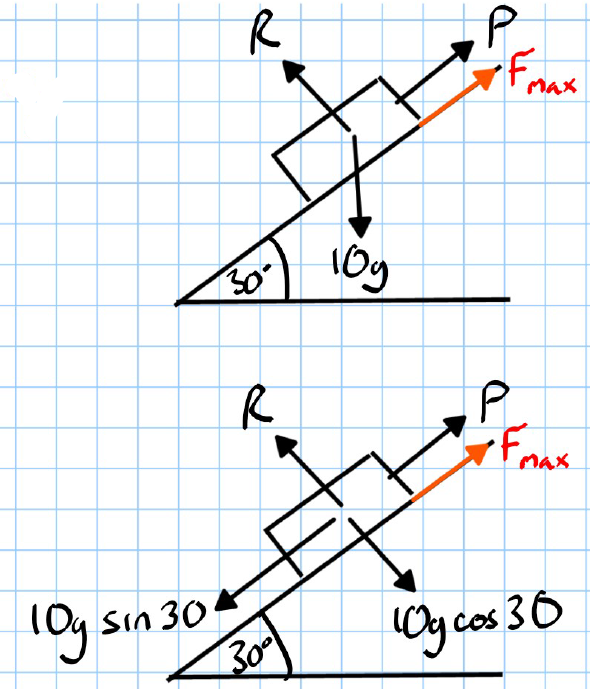
- Calculation:
Answer (a)****:
Part (b): On the Point of Moving Up the Slope
- Forces acting:
- Similar forces as in part (a), but friction now acts down the slope to oppose the motion.
- Equations of equilibrium:
- For horizontal equilibrium (resolving forces along the slope):
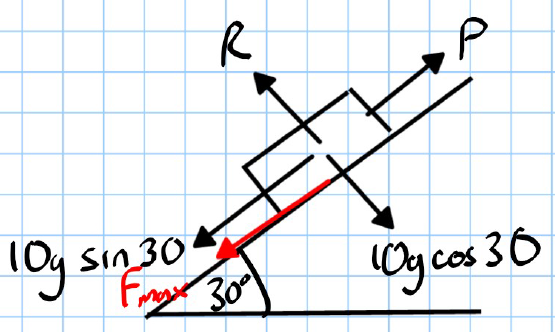
- Calculation:
Answer (b):
:::
500K+ Students Use These Powerful Tools to Master Coefficient of Friction - Inclined Planes For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
60 flashcards
Flashcards on Coefficient of Friction - Inclined Planes
Revise key concepts with interactive flashcards.
Try Maths Mechanics Flashcards6 quizzes
Quizzes on Coefficient of Friction - Inclined Planes
Test your knowledge with fun and engaging quizzes.
Try Maths Mechanics Quizzes5 questions
Exam questions on Coefficient of Friction - Inclined Planes
Boost your confidence with real exam questions.
Try Maths Mechanics Questions27 exams created
Exam Builder on Coefficient of Friction - Inclined Planes
Create custom exams across topics for better practice!
Try Maths Mechanics exam builder15 papers
Past Papers on Coefficient of Friction - Inclined Planes
Practice past papers to reinforce exam experience.
Try Maths Mechanics Past PapersOther Revision Notes related to Coefficient of Friction - Inclined Planes you should explore
Discover More Revision Notes Related to Coefficient of Friction - Inclined Planes to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Further Forces & Newton's Laws
Resolving Forces & Inclined Planes
332+ studying
182KViews96%
114 rated
Further Forces & Newton's Laws
Coefficient of Friction - F = ma
388+ studying
180KViews96%
114 rated
Further Forces & Newton's Laws
Coefficient of Friction - Harder Problems
424+ studying
181KViews