Photo AI
Last Updated Sep 26, 2025
Centres of Mass Simplified Revision Notes for A-Level AQA Maths Mechanics
Revision notes with simplified explanations to understand Centres of Mass quickly and effectively.
400+ students studying
4.1.3 Centres of Mass
Problem: Moments in 2 Dimensions
Given:
- A metal lever of mass 5 kg and length 1.5 m is attached by a smooth hinge to a vertical wall.
- The lever is held at an angle of 30° to the vertical by a horizontal force of magnitude F N applied at the other end of the lever.
- The lever is modeled as a uniform rod. Find: The value of F.
Solution:
Method 1: Changing Direction of Force
- Resolve forces into components parallel and perpendicular to the given distances.
- Weight of the lever 5g acts downward.
- Resolve the weight into two components:
- Perpendicular component: 5g sin(30°)
- Parallel component: 5g cos(30°)
- Force F is horizontal, and it is already perpendicular to the lever.
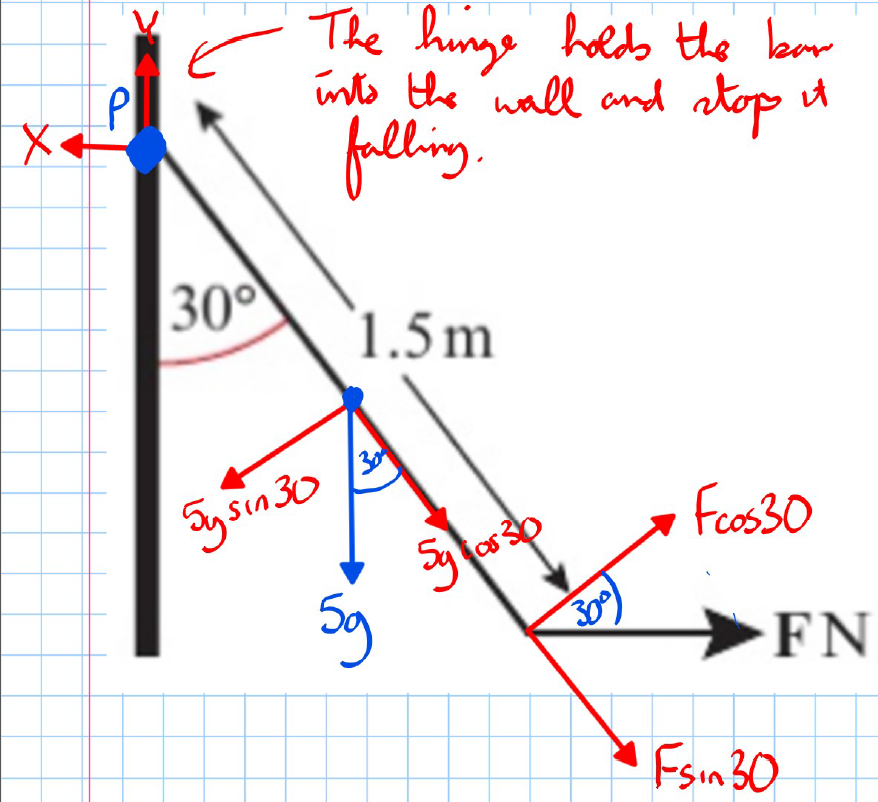
- Take moments about the pivot P:
- Taking clockwise moments as positive.
- Solve the resulting equation:
Simplifying:
Method 2: Resolve Perpendicular Distances
- Resolve distances perpendicular to the line of action of the forces.
- The perpendicular distance of the weight from the pivot P is 0.75 sin(30°).
- The perpendicular distance of F from the pivot P is 1.5 cos(30°).
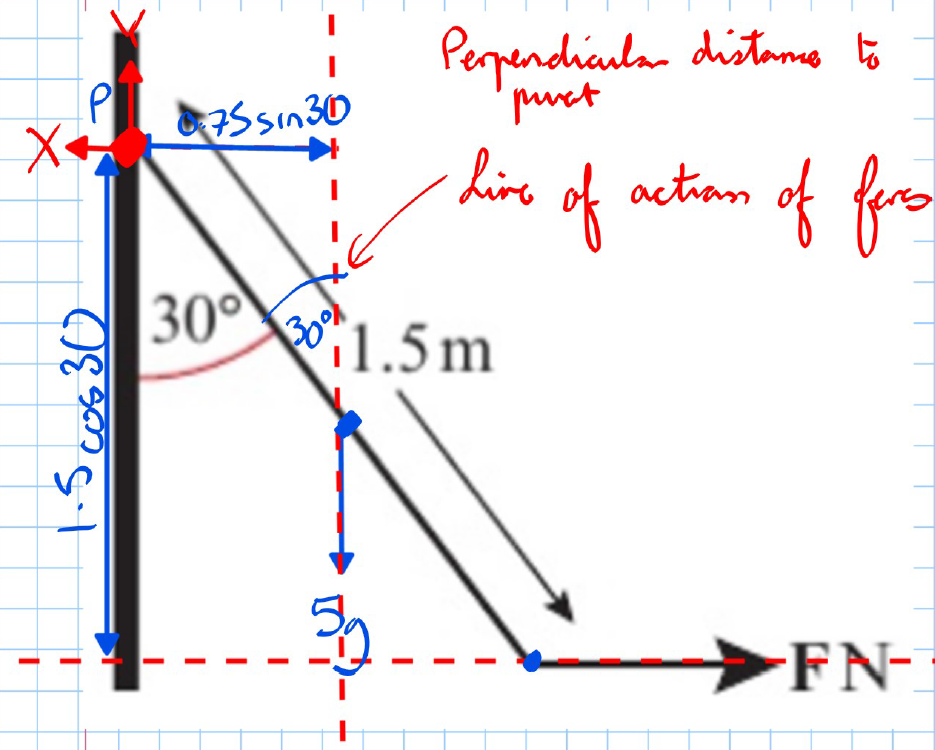
- Take moments about the pivot P:
- Solve the resulting equation: The calculation is the same as in Method 1, leading to:
Result: The value of F is approximately 14.15 N.
Tips:
- Draw a clear free body diagram: Identify all forces acting on the ladder, including:
- The weight of the ladder acting at its centre of mass.
- The normal reaction forces at the ground and the wall.
- Friction at the base (if applicable), which opposes slipping.
- Resolve forces and take moments: Resolve forces horizontally and vertically, applying equilibrium conditions ( ∑ Fx = 0 , ∑ Fy = 0). To solve for unknowns, take moments about a point, often the base of the ladder, where one or more forces pass through, eliminating them from the equation.
- Use friction carefully: For the ladder to remain in equilibrium, friction at the base must be sufficient to prevent slipping. Use F_friction = μN, where N is the normal force, and check if the friction is enough by comparing it with the horizontal forces.
500K+ Students Use These Powerful Tools to Master Centres of Mass For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
60 flashcards
Flashcards on Centres of Mass
Revise key concepts with interactive flashcards.
Try Maths Mechanics Flashcards6 quizzes
Quizzes on Centres of Mass
Test your knowledge with fun and engaging quizzes.
Try Maths Mechanics Quizzes5 questions
Exam questions on Centres of Mass
Boost your confidence with real exam questions.
Try Maths Mechanics Questions2 exams created
Exam Builder on Centres of Mass
Create custom exams across topics for better practice!
Try Maths Mechanics exam builder15 papers
Past Papers on Centres of Mass
Practice past papers to reinforce exam experience.
Try Maths Mechanics Past PapersOther Revision Notes related to Centres of Mass you should explore
Discover More Revision Notes Related to Centres of Mass to Deepen Your Understanding and Improve Your Mastery
