Photo AI
Last Updated Sep 27, 2025
Sketching Polynomials Simplified Revision Notes for A-Level AQA Maths Pure
Revision notes with simplified explanations to understand Sketching Polynomials quickly and effectively.
345+ students studying
2.7.1 Sketching Polynomials
Sketching Quartic Graphs
Characteristics of Different Degree Polynomials
-
A straight line (degree 1) has no turning points.
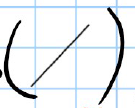
-
A quadratic (degree 2) has 1 turning point.

-
A cubic (degree 3) has up to 2 turning points.

-
A quartic (degree 4) has up to 3 turning points.

Example: Sketch the following quartic
- Find the roots (x-intercepts) where :
-
Set :
-
The roots are .
- Find the y-intercept (where ):
- Substitute :
- Draw the graph:
- Plot the x-intercepts .
- Plot the y-intercept .
- Draw a smooth curve passing through these points.
Important Note
- Positive Quartic:
- Starts from the top left and ends at the top right.
- Example: .
- Negative Quartic:
- Starts from the bottom left and ends at the bottom right.
- Example: .
Summary Steps for Sketching Quartic Graphs
- Find roots (-intercepts):
- Set and solve for .
- Find the y-intercept:
- Set and solve for .
- Determine the end behaviour:
- If the coefficient of is positive, the graph starts and ends at the top.
- If the coefficient of is negative, the graph starts and ends at the bottom.
- Sketch the graph:
- Plot the intercepts.
- Ensure the curve smoothly passes through these points and follows the correct end behaviour.
Sketching Cubic Graphs
A cubic graph can take one of two shapes depending on whether the coefficient of is positive or negative.
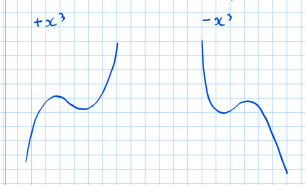
Shapes of Cubic Graphs
- Positive coefficient:
- The graph starts from the bottom left and ends at the top right.
- Negative coefficient:
- The graph starts from the top left and ends at the bottom right.
Example: Sketch 8. Find the roots (x-intercepts) where :
- Set
- The roots are .
- Find the y-intercept (where ):
- Substitute :
- Sketch the graph:
- Plot the x-intercepts .
- Plot the y-intercept .
- Draw a smooth curve passing through these points, starting from the bottom left (since the coefficient of is positive) and ending at the top right.
Points to Note
- Label all intercepts clearly on the graph.
- Ensure the curve does not go back on itself and smoothly passes through the intercepts.
- For the best example:
- Clearly mark the intercepts.
- Ensure the curve has the correct shape for the given cubic equation.
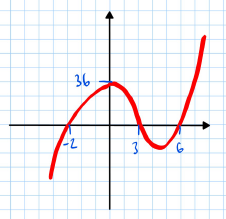
Correct and Incorrect Sketches
- Correct Sketch:
- Clearly labelled intercepts.
- Smooth curve passing through all intercepts.
- Correct end behaviour based on the coefficient of .
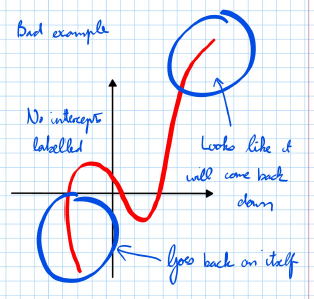
- Incorrect Sketch:
- No intercepts labelled.
- The curve going back on itself.
- The curve looking like it will come back down when it should not.
Sketching Cubic Graphs with Roots
Example 1: Sketch
- Find the roots (-intercepts) where :
-
Set :
-
The roots are .
- Find the y-intercept (where ):
- Substitute
- Sketch the graph:
- Plot the -intercepts .
- Plot the y-intercept .
- Draw a smooth curve passing through these points.
Example 2: Sketch
- Notice the double root:
- The equation has a double root at .
-
Rewrite the equation:
-
Find the roots (x-intercepts) where :
-
Set :
-
The roots are (double root), .
- Find the y-intercept (where ):
- Substitute :
- Sketch the graph:
- Plot the -intercepts .
- Plot the -intercept .
- Draw a smooth curve passing through these points, noting the double root behavior at .
Example 3: Sketch 16. Identify the triple root:
- The equation has a triple root at .
- Find the root (-intercept) where :
-
Set :
-
The root is .
- Find the y-intercept (where ):
- Substitute :
- Sketch the graph:
- Plot the -intercept .
- Plot the y-intercept .
- Draw a smooth curve passing through these points, noting the triple root behavior at .
Summary
- For single roots, the curve crosses the -axis.
- For double roots, the curve touches the -axis and turns around.
- For triple roots, the curve flattens at the -axis.
Standard Graphs
The shapes of the following graphs need to be learned:
1. Graph of
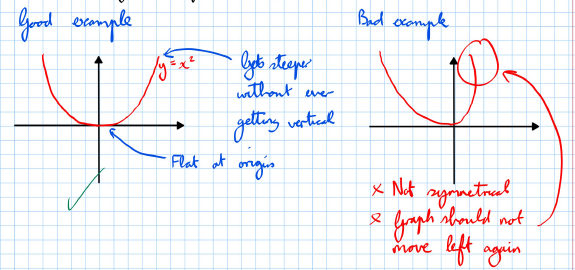
Good Example
- The graph is a parabola that opens upwards.
- It gets steeper but never becomes vertical.
- It is flat at the origin.
Bad Example
- The graph is not symmetrical.
- The graph should not move left again.
- It should be flat at the origin and smooth.
2. Graph of
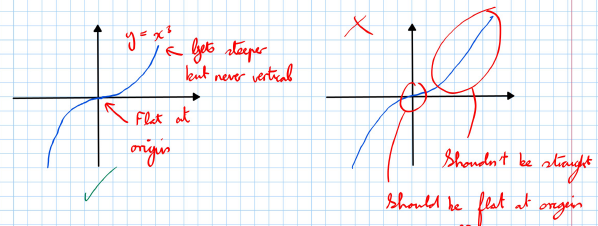
Good Example
- The graph starts from the bottom left and ends at the top right.
- It gets steeper but never becomes vertical.
- It is flat at the origin.
Bad Example
- The graph is not smooth.
- It should be flat at the origin.
- The graph should not go back on itself.
3. Graph of
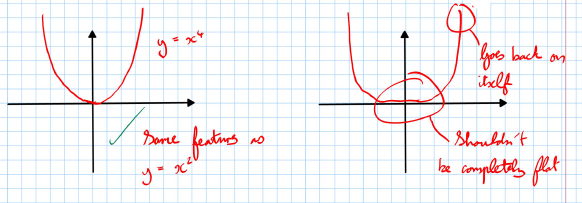
- This graph looks similar to but is steeper.
- It has the same basic shape and features.
4. Graph of
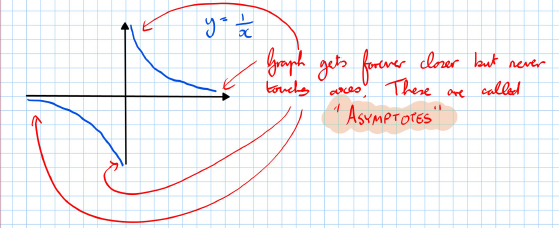
- The graph has two separate curves.
- It gets forever closer but never touches the axes.
- These lines it approaches but never touches are called asymptotes.
5. Graph of
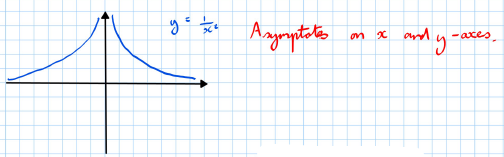
- The graph is symmetrical and has two separate curves.
- It has asymptotes on the x and y-axes.
6. Graph of
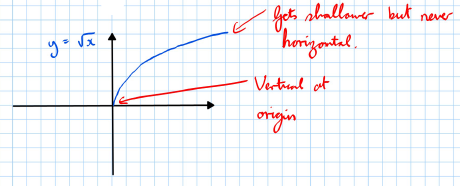
- The graph starts at the origin.
- It gets shallower but never becomes horizontal.
- It is vertical at the origin.
500K+ Students Use These Powerful Tools to Master Sketching Polynomials For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Sketching Polynomials
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards5 quizzes
Quizzes on Sketching Polynomials
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes23 questions
Exam questions on Sketching Polynomials
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Sketching Polynomials
Create custom exams across topics for better practice!
Try Maths Pure exam builder18 papers
Past Papers on Sketching Polynomials
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Sketching Polynomials you should explore
Discover More Revision Notes Related to Sketching Polynomials to Deepen Your Understanding and Improve Your Mastery
