Photo AI
Last Updated Sep 26, 2025
Language of Functions Simplified Revision Notes for A-Level AQA Maths Pure
Revision notes with simplified explanations to understand Language of Functions quickly and effectively.
267+ students studying
2.8.1 Language of Functions
Notation
Domain and Range of a Function
- The domain of a function is the set of values we are allowed to "feed" a function. Provided the function is defined, we are allowed to choose the domain.
Example:
-
This is the domain we have chosen.
-
A sketch of this graph would look like this: (Note: This sketch shows the line starting from and increasing.)
-
However, we have only allowed the function f to be defined for .
-
(Note: Point at is marked, illustrating that the function starts from this point.)
-
Notice, to illustrate the graph continues forever, the line has just vanished off the grid.
Example of an Incorrect Domain for a Real Function:
- This cannot be correct as the function is undefined for .
Range of a Function
- The range of a function is the set of y values can take, given a particular domain.
Example 1:
-
Sketch: for and state its range.
-
The sketch shows a parabola opening upwards with its vertex at . This helps in determining the range.
-
Calculator Steps:
- Input the quadratic formula.
- The discriminant shows no real roots, indicating the vertex is the minimum point.
- Minimum point calculation gives: and .
- Thus, the range is or .
Example 2:
-
Find the range of .
-
Sketch shows the exponential function starting from .
-
The blue highlight indicates the part of the function of interest.
-
, indicating that for .
-
The range is the set of all values such that .
The function is defined by for . The graph of is shown above.
- State the range of .
- At :
Thus, . The range of f is .
- Find the value of .
- First, calculate :
- Then, calculate :
Mapping
A function maps one set of numbers to another. The input is called the domain, the output set is called the range.
Example:
- Domain:
- Range:
From the above, we can construct the statement:
(beyond the space)
maps real numbers to real numbers greater than or equal to .
Taking some specific values of mapping:
Domain:
Range:
For :
- Notice that for each element of the range, there are two elements (i.e., many) that map to one element of the range.
For example, .
Thus, the function is MANY-TO-ONE or MANY-ONE.
You can classify a function as many-to-one by drawing the function and drawing a horizontal line through the function.
Example:
- Domain:
- Range:
Since the line intersects the curve twice, we can see graphically that one y value is obtained from many values.
Example of one-to-many:
One -value, e.g., , gives many -values (i.e., ).
Draw a vertical line to test for this. If the line cuts in more than one place at any point, the function is ONE-TO-MANY.
What type of function is the following:
Conclusion: This function is Many-to-Many.
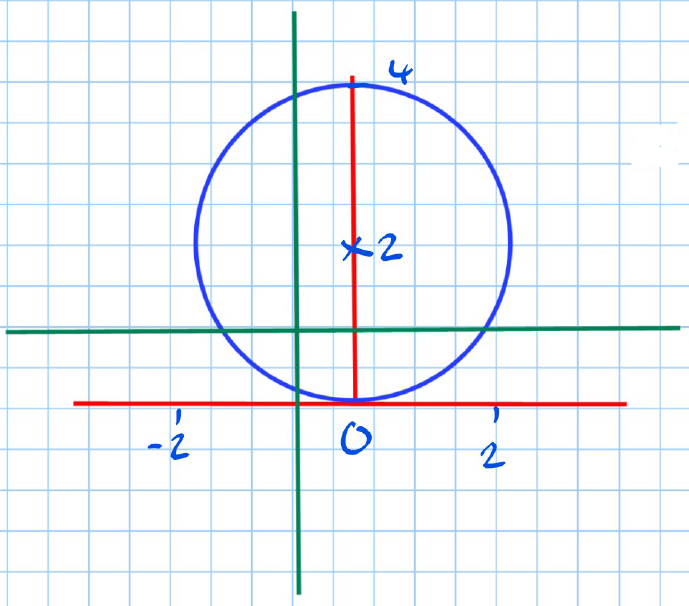
Explanation:
The significance of this is that a function that is Many-to-Many has no inverse. We cannot deduce a unique input from a given output.
Something is only strictly a function if it does not end "many," i.e., does end "one."
500K+ Students Use These Powerful Tools to Master Language of Functions For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
60 flashcards
Flashcards on Language of Functions
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards6 quizzes
Quizzes on Language of Functions
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes12 questions
Exam questions on Language of Functions
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Language of Functions
Create custom exams across topics for better practice!
Try Maths Pure exam builder18 papers
Past Papers on Language of Functions
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Language of Functions you should explore
Discover More Revision Notes Related to Language of Functions to Deepen Your Understanding and Improve Your Mastery
