Photo AI
Last Updated Sep 27, 2025
Binomial Expansion Simplified Revision Notes for A-Level AQA Maths Pure
Revision notes with simplified explanations to understand Binomial Expansion quickly and effectively.
287+ students studying
4.1.1 Binomial Expansion
Binomial Expansions
Binomial Theorem:
The binomial expansion is the process of expanding expressions of the form , where is a non-negative integer. The formula for the expansion is given by the Binomial Theorem:
Where:
- is the binomial coefficient, read as "n choose k," and is given by:
- is the factorial of .
- is the term involving , and is the term involving .
General Form of the Expansion:
The binomial expansion of will look like this:
Each term in the expansion consists of:
- Binomial Coefficient:
- A power of , starting from and decreasing to .
- A power of , starting from and increasing to .
Examples:
- Example 1: Expand :
Using the Binomial Theorem:
- The first term is , with a binomial coefficient of .
- The second term is , with a binomial coefficient of .
- The third term is , with a binomial coefficient of .
- Example 2: Expand :
Using the Binomial Theorem:
- The first term is , with a binomial coefficient of .
- The second term is , with a binomial coefficient of .
- The third term is , with a binomial coefficient of .
- The fourth term is , with a binomial coefficient of .
Binomial Coefficients:
The binomial coefficients are the numbers that appear in Pascal's Triangle, and they can be computed using the formula:
Where (factorial of ) is the product of all positive integers up to .
Pascal's Triangle:
Pascal's Triangle is a triangular array of numbers, where each number is the sum of the two directly above it. The -th row gives the binomial coefficients for .
For example, the first few rows of Pascal's Triangle are:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Properties of Binomial Expansion:
- The total number of terms in the expansion of is n + 1 .
- The sum of the exponents of and in each term is always .
- The binomial expansion can be applied to both positive and negative terms as long as is a non-negative integer.
Special Cases:
- For : The expansion follows the same pattern as , except the signs alternate.
- For fractional or negative exponents, the binomial expansion becomes an infinite series and requires more advanced methods (not covered in basic binomial expansion).
Applications of Binomial Expansion:
- Algebraic Expansion: Simplifying powers of binomials like
- Approximations: In cases where is large, binomial expansion helps in approximation methods.
- Probability: Binomial coefficients appear in binomial probability distributions.
Counting Combinations
- Picking 2 different colours from 4 colours:
- When the order of choosing is not important, we have:
- This is because there are 6 different ways to choose colours out of
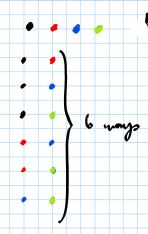
- Picking 3 different colours from 4 colours:
- Again, when the order of choosing is not important, we have:
- This is because there are 4 different ways to choose colours out of .
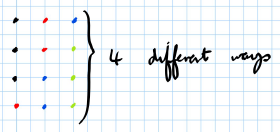
General Formula
The binomial coefficient (combinations) is given by:
Example Calculations
- Choosing out of :
Table of Combinations
| Number of Colours Chosen (from 4) | Number of Ways |
|---|---|
| 0 | 1 |
| 1 | 4 |
| 2 | 6 |
| 3 | 4 |
| 4 | 1 |
The formula for combinations ensures that we count the number of ways to choose items without regard to the order of selection.
500K+ Students Use These Powerful Tools to Master Binomial Expansion For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
20 flashcards
Flashcards on Binomial Expansion
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards2 quizzes
Quizzes on Binomial Expansion
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes13 questions
Exam questions on Binomial Expansion
Boost your confidence with real exam questions.
Try Maths Pure Questions2 exams created
Exam Builder on Binomial Expansion
Create custom exams across topics for better practice!
Try Maths Pure exam builder18 papers
Past Papers on Binomial Expansion
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Binomial Expansion you should explore
Discover More Revision Notes Related to Binomial Expansion to Deepen Your Understanding and Improve Your Mastery
Load more notes