4.4.2 Geometric Series

Infinite Geometric Series

So far we have only dealt with the sum of a finite number of terms of a geometric sequence. If certain conditions are fulfilled, then it is possible to sum an infinite number of terms of a geometric sequence.

The more terms we add, the bigger the sum gets without any upper bound.

$$\Rightarrow \text{As } n \rightarrow \infty, \quad S_n \rightarrow \infty$$

As the no. of terms increases, the sum of these terms approaches $\infty$.

In such circumstances, we say the series diverges.

---

e.g. Consider the series $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots$

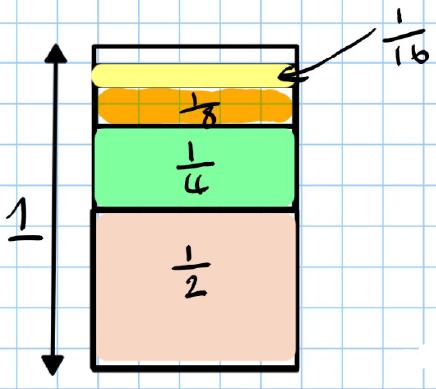
Consider filling a glass of capacity $1$ with the quantities in the above series. We see that the glass will get closer and closer to being full but never quite get there.

i.e.,

$$\text{As } n \rightarrow \infty, \quad S_n \rightarrow 1$$

As the no. of terms gets bigger, the sum of these terms approaches $1$.

In such circumstances, the series is said to converge.

---

Sum to Infinity

---

---

e.g. Find the sum of $6 + 2 + \frac{2}{3} + \frac{2}{9} + \ldots$

$a = 6$

$r = \frac{1}{3}$

The sequence converges since $-1 < \frac{1}{3} < 1$

$$\Rightarrow S_{\infty} = \frac{6}{1 - \frac{1}{3}} = 9$$

---

In a geometric progression, the sum to infinity is four times the first term.

(i) Show that the common ratio is $\frac{3}{4}$.

$$\frac{a}{1-r} = 4a \xRightarrow{x(1-r)} a = 4a(1-r) \xRightarrow{\div a} 1 = 4(1-r)\\ \Rightarrow 1 = 4 - 4r \Rightarrow 4r = 3 \Rightarrow r = \frac{3}{4}$$

(ii) Given that the third term is $9$, find the first term.

$$ar^2 = 9 \Rightarrow a\left(\frac{3}{4}\right)^2 = 9 \Rightarrow a = 16$$

(iii) Find the sum of the first twenty terms.

$$S_{20} = \frac{16 \left(1 - \left(\frac{3}{4}\right)^{20}\right)}{1 - \frac{3}{4}} = 63.797$$

---