Photo AI
Last Updated Sep 27, 2025
Small Angle Approximations Simplified Revision Notes for A-Level AQA Maths Pure
Revision notes with simplified explanations to understand Small Angle Approximations quickly and effectively.
419+ students studying
5.4.3 Small Angle Approximations
Small angle approximations are useful techniques in trigonometry and calculus for simplifying the values of trigonometric functions when the angle is small (typically measured in radians). These approximations are particularly helpful when dealing with limits, series expansions, or problems where the angle is close to zero.
1. Key Small Angle Approximations:
For very small angles (in radians), the following approximations hold:
- Sine:
- Cosine:
- Tangent:
2. Understanding the Approximations:
-
Sine Approximation: As approaches 0, the sine of the angle becomes nearly equal to the angle itself when is in radians. This is because the graph of is very close to the line y = for small values of .
-
Cosine Approximation: For small angles, remains close to 1, with the first correction term being . The cosine graph is nearly flat near which is why the approximation starts with 1.
-
Tangent Approximation: Since , and both and for small , the tangent function also approximates to the angle itself.
3. Derivation Using Taylor Series:
These approximations can be derived from the Taylor series expansions of the trigonometric functions around
- Sine:
For small , higher-order terms like become negligible, so:
- Cosine:
For small , higher-order terms like become negligible, so:
- Tangent:
4. Applications of Small Angle Approximations:
- Physics: Small angle approximations are frequently used in physics, particularly in pendulum motion, where the sine of the angle of displacement is approximated as the angle itself for small oscillations.
- Engineering: In engineering, small angle approximations simplify the analysis of structures and mechanisms where small angular displacements occur.
- Astronomy: The approximation is also used in astronomy for calculating the angular diameter of celestial objects when viewed from Earth.
5. Example Problems Using Small Angle Approximations:
Example 1: Approximate radians.
Using the small angle approximation:
The exact value , showing that the approximation is quite close.
Example 2: Approximate radians.
Using the small angle approximation:
The exact value which matches the approximation closely.
Example 3: Simplify for small \theta.
Using the small angle approximation:
This approximation is useful in limits, particularly in calculus when evaluating
Summary:
- Small angle approximations provide a powerful tool for simplifying trigonometric expressions when dealing with angles close to zero.
- They are derived from the Taylor series expansions of the trigonometric functions and are especially useful in physics, engineering, and calculus.
- Understanding these approximations allows for quicker and more intuitive problem-solving in scenarios where small angles are involved.
Small Angle Approximations
When dealing with small angles measured in radians, there are certain useful approximations we can use if the context of the problem allows approximations.
Graph: A graph is shown with two lines:
- The blue line represents .
- The red curve represents .
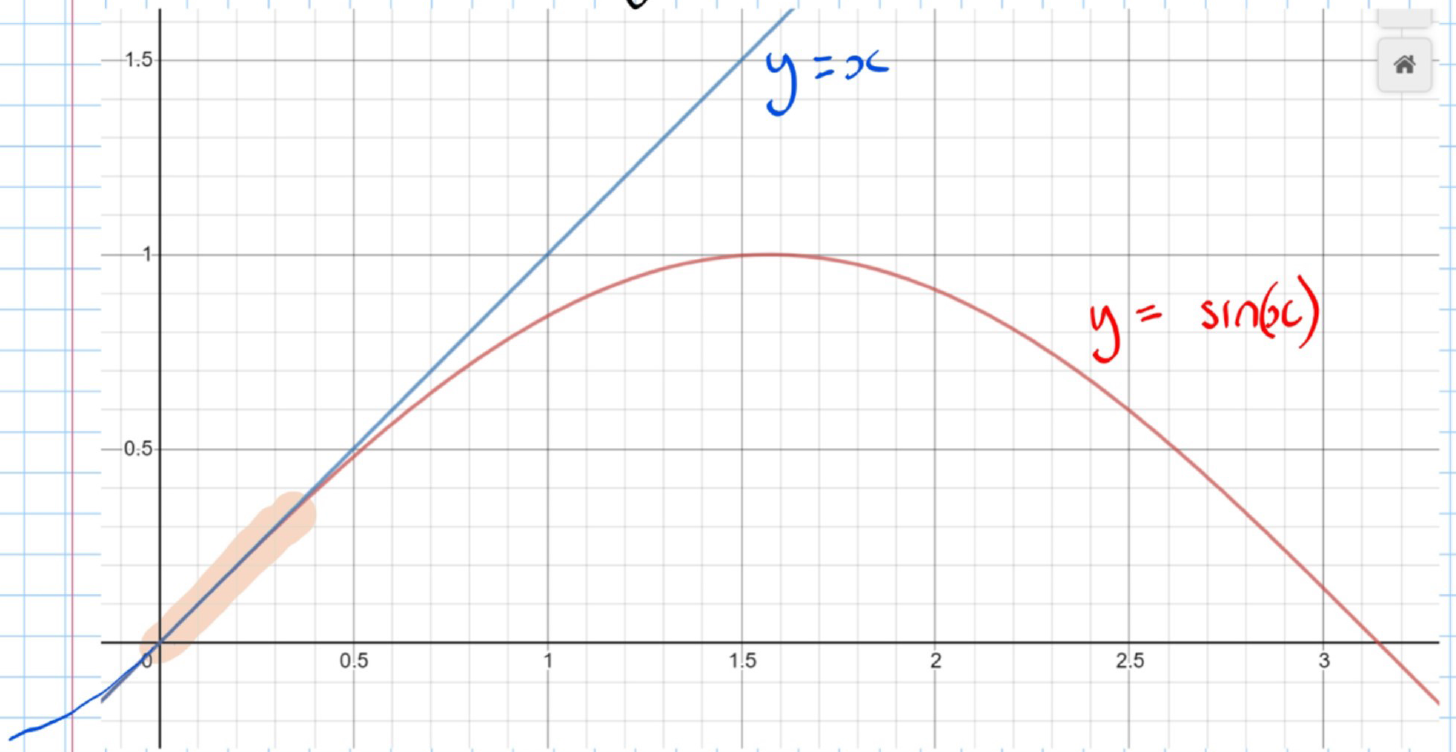
The above graph suggests that for small .
Using , we can derive another approximation for :
(Using double angle formula)
For small
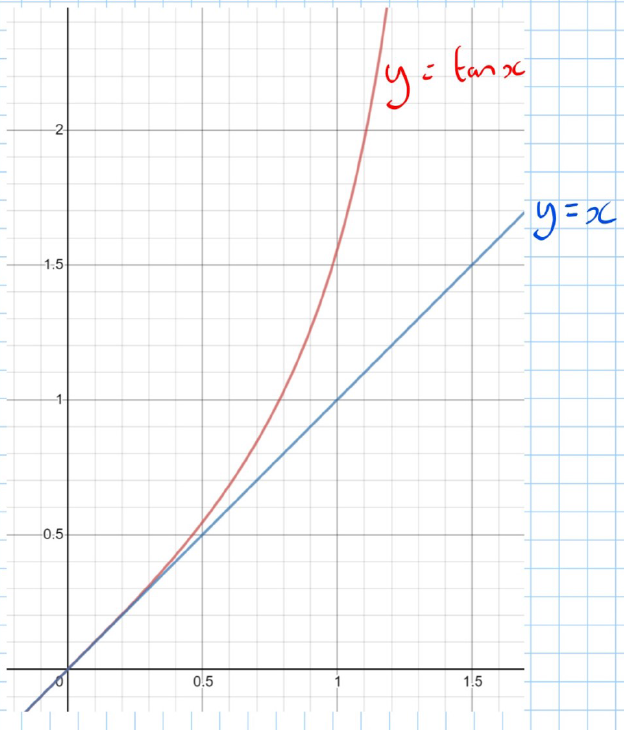
For small
Example Problem
- When is small, find the approximate values of: a)
Solution:
a) As
b) As
c) For small
2. When is small, show that:
a) For small ,
b) For small ,
c) For small ,
Q1 (OCR H240/03, Sample Question Paper, Q4) Show that, for a small angle , where is in radians,
Solution:
When is small,
As is small, is insignificantly small.
Q3, (OCR H240/02, Practice Paper Set 3, Q3) Use small angle approximations to estimate the solution of the equation:
if is small enough to neglect terms in or above.
When is small,
5. a) When is small, show that the expression
can be written as .
b) Hence write down the value of when is small.
When is small,
Assuming is small, we can approximate the expression as .
Hence when is small.
500K+ Students Use These Powerful Tools to Master Small Angle Approximations For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
40 flashcards
Flashcards on Small Angle Approximations
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards4 quizzes
Quizzes on Small Angle Approximations
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes10 questions
Exam questions on Small Angle Approximations
Boost your confidence with real exam questions.
Try Maths Pure Questions2 exams created
Exam Builder on Small Angle Approximations
Create custom exams across topics for better practice!
Try Maths Pure exam builder18 papers
Past Papers on Small Angle Approximations
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Small Angle Approximations you should explore
Discover More Revision Notes Related to Small Angle Approximations to Deepen Your Understanding and Improve Your Mastery
