Photo AI
Last Updated Sep 27, 2025
Stationary Points & Turning Points Simplified Revision Notes for A-Level AQA Maths Pure
Revision notes with simplified explanations to understand Stationary Points & Turning Points quickly and effectively.
267+ students studying
7.2.4 Stationary Points & Turning Points
Stationary points and turning points are crucial concepts in calculus that help in analysing the shape of a graph and determining where a function reaches its local maxima or minima. Understanding these points is essential for curve sketching, optimization, and understanding the behaviour of functions.
1. Stationary Points:
A stationary point on the graph of a function occurs where the derivative of the function is zero. Mathematically, if , then is a stationary point.
- Types of Stationary Points:
- Local Maximum: A point where reaches a local maximum value.
- Local Minimum: A point where reaches a local minimum value.
- Saddle Point (or Point of Inflection): point where the slope is zero but the function does not have a local maximum or minimum. The curve changes concavity at this point.
2. Finding Stationary Points:
To find stationary points of a function , follow these steps:
- Find the first derivative .
- Set the first derivative equal to zero and solve for :
- Find the corresponding y-coordinates by substituting the values of back into the original function .
- Classify the stationary points using the second derivative test or first derivative test.
3. Turning Points:
A turning point is a type of stationary point where the function changes direction, meaning the function switches from increasing to decreasing (local maximum) or from decreasing to increasing (local minimum). All turning points are stationary points, but not all stationary points are turning points (e.g., saddle points are not turning points).
- Local Maximum: The graph changes from increasing to decreasing at a turning point.
- Local Minimum: The graph changes from decreasing to increasing at a turning point.
4. Classifying Stationary Points:
a) Second Derivative Test:
The second derivative test can help classify stationary points:
- If at a stationary point , then has a local minimum at .
- If at a stationary point , then has a local maximum at .
- If at a stationary point , the test is inconclusive, and you may need to use higher derivatives or another method to classify the point.
b) First Derivative Test:
The first derivative test involves checking the sign of before and after the stationary point:
- If changes from positive to negative as passes through the stationary point, then has a local maximum at that point.
- If changes from negative to positive, then has a local minimum.
- If does not change sign (e.g., it remains positive or negative), the stationary point is a saddle point (not a turning point).
5. Example Problems:
Example 1: Find and classify the stationary points of .
- Step 1: Find the first derivative:
- Step 2: Find the stationary points by setting :
So, and are stationary points.
- Step 3: Classify the stationary points using the second derivative test.
- First, find the second derivative:
- Evaluate at the stationary points:
- At is a local maximum.
- At is a local minimum.
- Step 4: Find the corresponding y-values:
- At .
- At .
- Conclusion:
- The stationary point at (0, 2) is a local maximum.
- The stationary point at (2, -2) is a local minimum.
Example 2: Find and classify the stationary points of .
- Step 1: Find the first derivative:
- Step 2: Find the stationary points by setting :
So, , and are stationary points.
- Step 3: Classify the stationary points using the second derivative test.
- First, find the second derivative:
- Evaluate at the stationary points:
- At (local minimum).
- At (local maximum).
- At (local minimum).
- Step 4: Find the corresponding -values:
- At .
- At .
- At .
- Conclusion:
- The stationary point at (0, 0) is a local minimum.
- The stationary point at (1, 1) is a local maximum.
- The stationary point at (2, 0) is a local minimum.
6. Applications of Stationary and Turning Points:
- Optimization: Finding maximum or minimum values of a function, which is essential in various fields such as economics, engineering, and physics.
- Curve Sketching: Understanding the shape and key features of the graph of a function.
- Physics: Analysing motion, especially when dealing with positions, velocities, and accelerations.
Summary:
- Stationary points occur where the first derivative of a function is zero, and they can be classified as local maxima, minima, or saddle points.
- Turning points are specific types of stationary points where the function changes direction, marking local maxima or minima.
- The second derivative test helps in classifying these points by determining the concavity of the function around them.
- Understanding stationary and turning points is crucial for analysing and interpreting the behaviour of functions in various mathematical and real-world contexts.
Differentiation: Stationary Points
A stationary point is a point on a graph that has zero gradient.
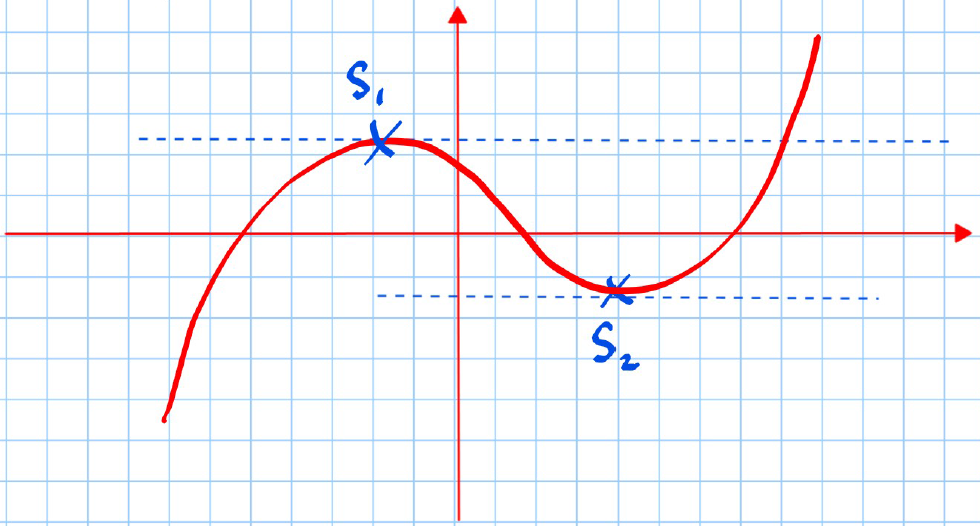
is called a local maximum.
- "Maximum" because it is the highest point in the locality.
- "Local" because it is not the maximum of the entire graph. is called a local minimum for similar reasons.
A stationary point that is the max/min of the entire function is called a Global max/min.
Example: Find the coordinates of the stationary points of .
- Differentiate to find the gradient function.
- Solve for :
- If asked, go back to coordinate equations to find y coordinates:
- When :
- When :
Classifying Stationary Points
At a known stationary point:
- If Min
- If Max
- If No information have to experiment numerically.
Example: Find and classify the stationary points of .
- Find (Worth 1 mark)
- When . When .
Now, classifying the points:
- At Min at (2, -16). (Worth a mark)
At Max at (-2, 16).
Example: Find and classify any stationary points of
- When this happens, we must test the gradient slightly to the left and slightly to the right of the stationary point:
- Left:
- Right:
Find and classify the stat. point of
- , which at gives Left:
Right:
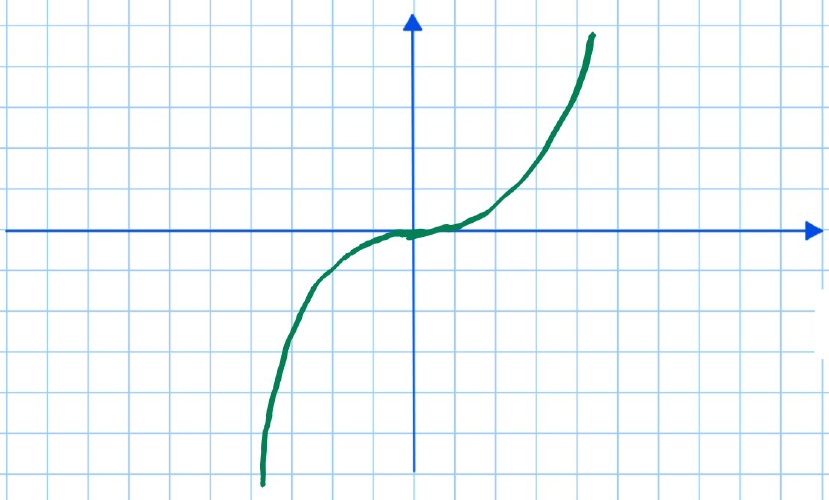
Note that max and min points can also be called "Turning Points".
500K+ Students Use These Powerful Tools to Master Stationary Points & Turning Points For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
70 flashcards
Flashcards on Stationary Points & Turning Points
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards7 quizzes
Quizzes on Stationary Points & Turning Points
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes24 questions
Exam questions on Stationary Points & Turning Points
Boost your confidence with real exam questions.
Try Maths Pure Questions1 exams created
Exam Builder on Stationary Points & Turning Points
Create custom exams across topics for better practice!
Try Maths Pure exam builder18 papers
Past Papers on Stationary Points & Turning Points
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Stationary Points & Turning Points you should explore
Discover More Revision Notes Related to Stationary Points & Turning Points to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Applications of Differentiation
Gradients, Tangents & Normal
396+ studying
192KViews96%
114 rated
Applications of Differentiation
Increasing & Decreasing Functions
391+ studying
182KViews96%
114 rated
Applications of Differentiation
Sketching Gradient Functions
442+ studying
184KViews