3.1.2 Venn Diagrams

Venn diagrams are a visual tool used to represent the relationships between different sets of data. They are especially useful in set theory, probability, and logic to show how different groups or sets overlap and interact with each other.

Components of a Venn Diagram

Circles: Each circle represents a set. The elements (or members) of the set are usually placed inside the circle.
Intersection: The area where two or more circles overlap represents the elements that are common to those sets.
Union: The area covered by all circles combined represents all the elements that are in any of the sets.
Complement: The area outside a particular circle represents the elements not in that set.

infoNote

Example with Two Sets: Let's consider two sets:

Set A: Students who play football.
Set B: Students who play basketball. A Venn diagram with these two sets would have two circles:
Circle A: Represents all students who play football.
Circle B: Represents all students who play basketball.
The overlapping area (intersection) represents students who play both football and basketball.

Notation

Union $(A \cup B)$ : The set of elements that are in A, B, or both. This is represented by the entire area covered by both circles.
Intersection $(A \cap B)$ : The set of elements that are in both A and B. This is represented by the overlapping area of the circles.
Complement $(A')$ : The set of elements that are not in A. This is the area outside circle A.

infoNote

Example: Suppose:

Set A: { $1, 2, 3, 4$ }
Set B: { $3, 4, 5, 6$ }
Union $(A \cup B)$ : { $1, 2, 3, 4, 5, 6$ }
Intersection $(A \cap B)$ : { $3, 4$ }
Complement of A $(A')$ : All elements not in set A (this could depend on the universal set, which might be, say, { $1, 2, 3, 4, 5, 6, 7, 8, 9, 10$ }.

Venn Diagrams with Three Sets

When dealing with three sets (A, B, and C), the Venn diagram consists of three overlapping circles. This allows you to represent the intersection of any combination of the sets.

infoNote

Example: Let's say:

Set A: Students who play football.
Set B: Students who play basketball.
Set C: Students who play tennis. The Venn diagram will show:
The areas where only A and B overlap (students who play both football and basketball, but not tennis).
The areas where only B and C overlap (students who play both basketball and tennis, but not football).
The areas where all three sets overlap (students who play football, basketball, and tennis).

Practical Uses

Probability: Venn diagrams help in visualising and calculating the probability of combined events.
Set Theory: They are fundamental in understanding operations like union, intersection, and difference of sets.
Logic and Reasoning: Venn diagrams are used to illustrate logical relationships and test the validity of arguments.

infoNote

Example: Consider the following data:

$30$ students play football.
$25$ students play basketball.
$15$ students play both football and basketball. To represent this in a Venn diagram:
Draw two overlapping circles.
Place $15$ in the intersection (students who play both).
Place $30 - 15 = 15$ in the football-only part of the football circle.
Place $25 - 15 = 10$ in the basketball-only part of the basketball circle.

Explanation:

The Venn diagram helps understand and calculate the number of students who play only one sport or both.
Venn diagrams are powerful tools for visualising relationships between sets and simplifying complex problems, especially in probability and logical reasoning.

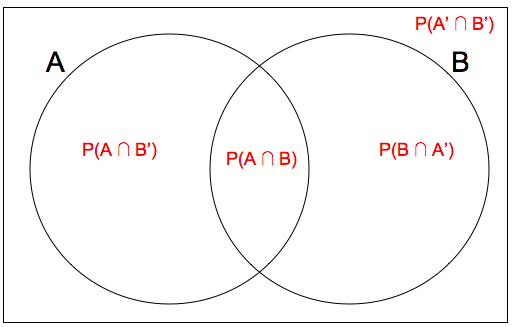
Conditional Probabilities from Venn Diagrams

infoNote

Example Questions

A Venn diagram is provided with probabilities for two events A and B.

The tasks are to find the following probabilities:

a) $P(A \cup B)$
b) $P(A | B)$
c) $P(B | A')$
d) $P(B | A \cup B)$

Worked Solutions

Finding $P(A \cup B)$ :

P(A \cup B) = 0.3 + 0.12 + 0.28 = :success[0.7]

This represents the probability that either event $A$ or $B$ or both occur.

b. Finding $P(A | B)$ :

$P(A | B)$ means "the probability that $A$ occurs, given that $B$ occurs."

Given B has occurred, the denominator is the sum of the probabilities in event B.

P(A | B) = \frac{P(A \cap B)}{P(B)} = \frac{0.12}{0.12 + 0.28} = :success[\frac{3}{10}]

This is also shown using the formula for conditional probability:

P(A | B) = \frac{P(A \cap B)}{P(B)}.

c. Finding $P(B | A')$ :

$P(B | A')$ means the probability that $B$ occurs given that $A$ does not occur.

P(B | A') = \frac{0.28}{0.58}\quad \text {simplifies to} \quad :success[\frac{14}{29}].

d. Finding $P(B | A \cup B)$ :

First, calculate the probability of the intersection of B with $A \cup B$ :

P(B \cap (A \cup B)) = P(B) = 0.12 + 0.28

Then, calculate the probability of $A \cup B$ :

P(A \cup B) = 0.3 + 0.12 + 0.28 = 0.7

Finally, apply the formula for conditional probability:

P(B | A \cup B) = \frac{P(B)}{P(A \cup B)} = \frac{0.12 + 0.28}{0.7} = :success[\frac{6}{7}]

This gives the final answer as $\frac{6}{7}$ .

Venn Diagrams Simplified Revision Notes for A-Level AQA Maths Statistics

3.1.2 Venn Diagrams

Components of a Venn Diagram

Notation

Venn Diagrams with Three Sets

Practical Uses

Conditional Probabilities from Venn Diagrams

Example Questions

Worked Solutions

500K+ Students Use These Powerful Tools to Master Venn Diagrams For their A-Level Exams.

Other Revision Notes related to Venn Diagrams you should explore