Photo AI
Last Updated Sep 27, 2025
The discovery of photoelectricity Simplified Revision Notes for A-Level AQA Physics
Revision notes with simplified explanations to understand The discovery of photoelectricity quickly and effectively.
326+ students studying
12.2.4 The discovery of photoelectricity
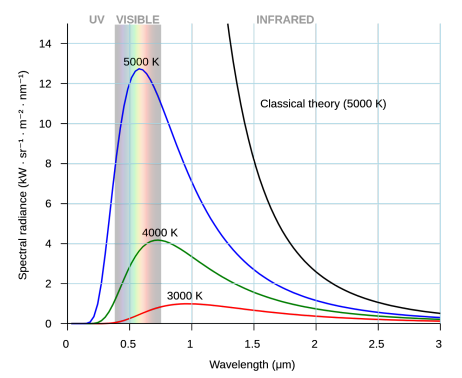
1. Background: Black Body Radiation and the UV Catastrophe
- A black body absorbs and emits radiation across all possible wavelengths. Classical wave theory predicted that as wavelength decreased, intensity of emitted radiation should increase, theoretically resulting in an infinite amount of ultraviolet radiation. However, this was not observed in experiments.
- This discrepancy became known as the ultraviolet catastrophe, showing that the wave theory of light could not explain observed data accurately.
- Planck's Solution:
- Planck suggested that electromagnetic (EM) waves exist in discrete packets of energy, known as quanta. The energy of each quantum is directly proportional to its frequency, described by the equation:
- Here, is energy, is Planck's constant, and is frequency. This quantisation helped resolve the UV catastrophe and formed a basis for quantum mechanics.
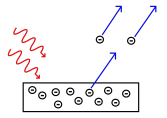
2. The Photoelectric Effect
- Overview: The photoelectric effect occurs when light shining on a metal surface causes electrons to be emitted from that surface.
- Wave theory failed to explain certain observations in the photoelectric effect:
- Threshold Frequency: Wave theory would suggest any light frequency should cause emission if intensity is high enough, but experimentally, only light above a certain frequency caused electron emission. This minimum frequency is called the threshold frequency.
- Instantaneous Emission: Electron emission was observed immediately when the light was turned on, contradicting wave theory, which would predict a delay as energy accumulates.
- Intensity and Kinetic Energy: Increasing light intensity raised the number of electrons emitted per second but did not increase the kinetic energy of individual electrons, contrary to what wave theory would predict.
- Variety of Kinetic Energies: Photoelectrons were emitted with a range of kinetic energies, which was not explainable by the wave model.
3. Einstein's Photon Model and Explanation of the Photoelectric Effect
- Photon Model: Einstein proposed that light is made up of particles, or photons, each carrying energy .
- Photon-Electron Interaction:
- When a photon collides with an electron, all of the photon's energy is transferred to the electron. If this energy exceeds the work function (the minimum energy needed to release an electron from the metal), an electron is emitted.
- The work function represents the binding energy of the electron to the metal surface. Only photons with energy can cause electron emission.
Key Points Explained by the Photon Model:
- Threshold Frequency: The energy of each photon must exceed the work function for emission to occur, thus only light with frequency above the threshold will cause photoemission.
- Instant Emission: As soon as a photon with sufficient energy strikes an electron, emission occurs without delay.
- Intensity and Rate of Emission: Higher light intensity means more photons, which increases the number of photoelectrons emitted per second but does not affect their energy.
- Range of Kinetic Energies: Photoelectrons emitted from deeper layers in the metal lose energy through collisions, so not all have the same kinetic energy upon reaching the surface.
4. Experimental Evidence Supporting the Photon Model
- Stopping Potential and Kinetic Energy:
- When a positive potential is applied across a metal surface, it attracts electrons back, requiring electrons to do work to overcome this potential. The stopping potential is the voltage needed to halt the electrons with the highest kinetic energy.
- The maximum kinetic energy of photoelectrons can be calculated from:
where is the elementary charge.
- Substituting into Einstein's photoelectric equation allows:
which can be rearranged to:
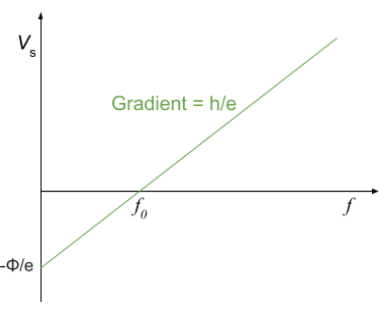
- Graphical Representation:
- A graph of stopping potential against frequency yields a straight line with:
- x-intercept represents the threshold frequency , the minimum frequency for photoemission.
500K+ Students Use These Powerful Tools to Master The discovery of photoelectricity For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
60 flashcards
Flashcards on The discovery of photoelectricity
Revise key concepts with interactive flashcards.
Try Physics Flashcards6 quizzes
Quizzes on The discovery of photoelectricity
Test your knowledge with fun and engaging quizzes.
Try Physics Quizzes29 questions
Exam questions on The discovery of photoelectricity
Boost your confidence with real exam questions.
Try Physics Questions27 exams created
Exam Builder on The discovery of photoelectricity
Create custom exams across topics for better practice!
Try Physics exam builder56 papers
Past Papers on The discovery of photoelectricity
Practice past papers to reinforce exam experience.
Try Physics Past PapersOther Revision Notes related to The discovery of photoelectricity you should explore
Discover More Revision Notes Related to The discovery of photoelectricity to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Wave-particle duality
Newton’s corpuscular theory of light
489+ studying
186KViews96%
114 rated
Wave-particle duality
Significance of Young’s double slit experiment
404+ studying
191KViews