Photo AI
Last Updated Sep 27, 2025
Time dilation Simplified Revision Notes for A-Level AQA Physics
Revision notes with simplified explanations to understand Time dilation quickly and effectively.
280+ students studying
12.3.3 Time dilation
Time Dilation
- Definition: Time dilation is an effect predicted by Einstein's theory of special relativity. It states that time will run at different rates for observers in different frames of reference, particularly when they are moving at high velocities relative to one another.
- Key Principle: Time dilation only occurs in inertial frames (frames moving at a constant velocity) and causes time to pass slower for an observer in motion relative to a stationary observer.
Key Concepts:
- Stationary Observer vs External Observer:
- The stationary observer is considered to be at rest relative to the event being measured.
- The external observer is moving relative to the stationary observer's frame of reference.
- Proper Time (): Time experienced by the stationary observer.
- Dilated Time (): Time experienced by the external observer (observed to be longer than proper time).
- Time Dilation Formula:
Where:
- = time observed by the external observer
- = proper time observed by the stationary observer
- = relative velocity between the observers
- = speed of light
- Important Note: The proper time will always be less than the dilated time observed by the external observer.
Example Problem:
- Problem: Suppose Lucy is on a spaceship traveling at 90% of the speed of light and measures a duration of 1 hour using her clock. How much time will pass on Earth during her measurement?
- Solution:
- Lucy is the stationary observer (relative to her own clock).
- Earth acts as the external observer because it is moving relative to Lucy.
- Given hour and ,
- Thus, while Lucy observes 1 hour passing, approximately 2.3 hours pass on Earth.
Experimental Evidence: Muon Decay
- Muon Decay provides practical evidence of time dilation. Muons are high-speed particles that enter Earth's atmosphere from space and decay very quickly.
- Experiment Setup: Detectors are placed at two altitudes to measure muon count rate, allowing for calculation of the time dilation effect on their decay.
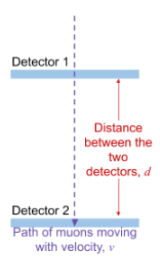
Experimental Setup for Muon Decay Observation
- Detector Placement:
- A detector is placed at a high altitude, and a detector is set up further down, closer to the Earth's surface.
- The distance between the two detectors is 2 km.
- Observations:
- Count rate at detector $1: 100 muons per second.
- Count rate at detector $2: 80 muons per second.
- Known Values:
- Muon speed : 0.996 times the speed of light .
- Muon half-life (at rest): 1.5 μs (or seconds.
Calculating Expected Count Rate at Detector 2
This experiment involves two calculations:
- Without considering special relativity (assuming no time dilation).
- Considering special relativity (accounting for time dilation).
1. Expected Count Rate at Detector (Ignoring Time Dilation)
- Step 1: Calculate the time for muons to travel between the detectors:
- Step 2: Calculate the number of half-lives expected during this time:
- Step 3: Determine the expected count rate at detector :
- Using the formula for exponential decay:
- Conclusion: This predicted count rate of 4.5 s⁻¹ is significantly lower than the observed 80 s⁻¹, suggesting that ignoring special relativity leads to an incorrect result.
2. Expected Count Rate at Detector 2 (Considering Time Dilation)
- Step 1: Calculate the time from the laboratory frame (external observer's perspective):
- Step 2: Calculate the proper time , which is the time experienced by the muons (moving frame):
- Substitute values:
- Step 3: Calculate the number of half-lives that occur during the muon's proper time:
- Step 4: Determine the expected count rate at detector :
- Using exponential decay:
- Conclusion: This value (76 s⁻¹) is much closer to the observed value of 80 s⁻¹, which supports the existence of time dilation as predicted by special relativity.
Muon Decay Example:
- Without considering relativity:
- Calculate time to travel between detectors.
- Predict muon count rate at lower detector without time dilation.
- Result: Calculations do not match observed data, indicating an issue.
- With time dilation:
- Calculate proper time using dilation formula.
- Predict count rate considering time dilation.
- Result: Calculations now closely match observed data, supporting relativity.
500K+ Students Use These Powerful Tools to Master Time dilation For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Time dilation
Revise key concepts with interactive flashcards.
Try Physics Flashcards5 quizzes
Quizzes on Time dilation
Test your knowledge with fun and engaging quizzes.
Try Physics Quizzes29 questions
Exam questions on Time dilation
Boost your confidence with real exam questions.
Try Physics Questions27 exams created
Exam Builder on Time dilation
Create custom exams across topics for better practice!
Try Physics exam builder56 papers
Past Papers on Time dilation
Practice past papers to reinforce exam experience.
Try Physics Past PapersOther Revision Notes related to Time dilation you should explore
Discover More Revision Notes Related to Time dilation to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Special relativity
Einstein’s Theory of Special Relativity
332+ studying
180KViews