Photo AI
Last Updated Sep 27, 2025
Young modulus Simplified Revision Notes for A-Level AQA Physics
Revision notes with simplified explanations to understand Young modulus quickly and effectively.
251+ students studying
4.2.2 Young modulus
Definition of Young Modulus
- The Young modulus (E) quantifies the stiffness of a material. It is a measure of a material's resistance to deformation under stress.
- For materials that obey Hooke's law (up to the limit of proportionality), stress is directly proportional to strain. This constant ratio of stress to strain is what defines the Young modulus.
Formula for Young Modulus
- The Young modulus can be defined as:
- Breaking down this relationship:
- Tensile Stress: The force per unit cross-sectional area applied to stretch or compress the material.
- Tensile Strain: The ratio of the extension of the material to its original length.
- Using formulas from stress and strain:
Where:
- = applied force (),
- = original length (),
- = cross-sectional area (),
- = extension ().
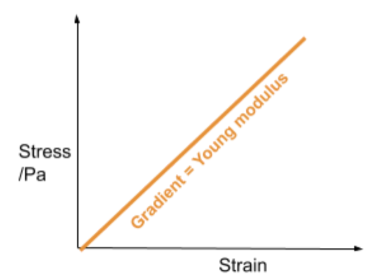
Finding Young Modulus from a Stress-Strain Graph
- On a stress-strain graph, the gradient of the straight-line portion (where Hooke's law is obeyed) represents the Young modulus.
- Gradient = Young modulus
- This part of the graph typically shows a linear relationship between stress and strain, indicating the material's proportionality limit.
Example Calculation of Young Modulus
Suppose we have a material with the following data:
Force applied () = N,
Original length () = m,
Cross-sectional area () = ,
Extension () = .
To find the Young modulus ():
- Substitute the values into the formula:
- Calculate each part:
- Numerator:
- Denominator:
- Divide:
So, the Young modulus of the material is MPa (megapascals).
Importance of Young Modulus
- Young modulus helps in assessing whether a material is suitable for specific structural applications where resistance to deformation is crucial.
- A high Young modulus indicates a stiff material that does not easily deform, like steel.
- A low Young modulus suggests a flexible material, such as rubber.
500K+ Students Use These Powerful Tools to Master Young modulus For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
20 flashcards
Flashcards on Young modulus
Revise key concepts with interactive flashcards.
Try Physics Flashcards2 quizzes
Quizzes on Young modulus
Test your knowledge with fun and engaging quizzes.
Try Physics Quizzes29 questions
Exam questions on Young modulus
Boost your confidence with real exam questions.
Try Physics Questions27 exams created
Exam Builder on Young modulus
Create custom exams across topics for better practice!
Try Physics exam builder56 papers
Past Papers on Young modulus
Practice past papers to reinforce exam experience.
Try Physics Past PapersOther Revision Notes related to Young modulus you should explore
Discover More Revision Notes Related to Young modulus to Deepen Your Understanding and Improve Your Mastery
