Determination of Young's Modulus

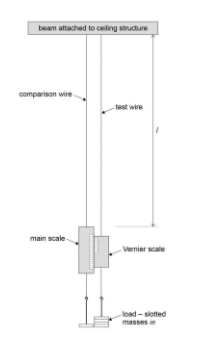
Two steel wires ( $1.5$ m each): One for testing and one as a reference to control for effects such as sagging.
Main scale and vernier scale: To measure the extension of the test wire accurately.
$1$ kg masses and holders: Used to apply force incrementally to the test wire.
Micrometer: To measure the diameter of the test wire for calculating the cross-sectional area.
Metre ruler: For measuring the initial length of the test wire.

infoNote

Arrange the apparatus as shown in the diagram, with both the test wire and the reference wire attached to the beam.
Measure the initial length $l$ of the test wire with the metre ruler.

Attach a 1 kg mass to both wires to make them taut, and record the initial reading on the scale for the test wire.

Add an additional 1 kg mass to the test wire only. Record the new scale reading and calculate the extension $e$ by subtracting the initial reading.
Repeat this process, adding 1 kg at a time up to around 8 kg, and measure the extension for each mass.

Repeat the experiment twice more for each mass to find the mean extension $e$ for each applied load $m$ .

Measure the diameter $d$ of the test wire at several points along its length using the micrometer. Take the mean value to calculate the cross-sectional area $A$ .

Using the average diameter $d$ , calculate the cross-sectional area $A$ of the wire:

A = \frac{\pi d^2}{4}

For each mass $m$ , calculate the force $F$ applied on the test wire by using $F = mg$ , where g ≈ 9.81 m/s².

Plot a graph of force $F$ on the y-axis against extension $e$ on the x-axis.
Draw a line of best fit. The gradient $G$ of this graph represents $\frac{F}{e}$ .

E = \frac{\text{stress}}{\text{strain}} = \frac{F/A}{e/l} = \frac{l \times G}{A}

Multiply the gradient $G$ by the initial length $l$ and divide by the cross-sectional area $A$ to determine $E$ .

infoNote

Wire Tension: The wire will be stretched tightly and could snap, which could injure eyes or other parts of the body. Wear safety goggles during the experiment.
Falling Weights: If the wire breaks, the weights may fall. Place a sand tray beneath the masses to cushion any potential impact.

Comparison Wire: The reference wire compensates for any sagging of the beam or thermal expansion. This ensures that only the test wire's extension is measured.
Length Accuracy: Use a long test wire (1.5 m or more) to minimise errors in measuring small extensions and to reduce percentage uncertainty in length measurements.

infoNote

Young Modulus $E$ : A measure of stiffness, calculated as the ratio of stress (force per unit area) to strain (extension per unit length).
Stress and Strain Relationship: Under small deformations, Hooke's Law applies, meaning stress is proportional to strain, and the constant of proportionality is $E$ .
Graphical Analysis: The gradient of the force vs. extension graph provides a proportional relationship, allowing us to calculate $E$ for the material.

Determination of Young's Modulus Simplified Revision Notes for A-Level AQA Physics