Photo AI
Last Updated Sep 27, 2025
Matrix Dimensions Simplified Revision Notes for A-Level Edexcel Further Maths Core Pure
Revision notes with simplified explanations to understand Matrix Dimensions quickly and effectively.
431+ students studying
2.1.2 Matrix Dimensions
The size or dimension of a matrix is defined by the number of rows and columns it contains. If a matrix has rows and columns, it is referred to as an matrix.
Example: The matrix
has rows and columns, so it is a matrix.
Matrices in 3-D
The 3D identity matrix is:
Any 3D linear transformation can be represented by a matrix in which the three columns are the images of the points , and , respectively.
For example, if under a linear transformation the point
then the matrix representing this transformation is:
The determinant of a 3D matrix representing a linear transformation is the scale factor of the change in volume of the original shape.
Example: Find the volume of the image of a cube of volume after being transformed by the matrix:
Using the calculator to do the determinant calculation for volume in 3D:
=
The volume of the new shape is , and the orientation has changed (since the determinant is negative).
3D Reflection Matrices
When reflecting in 3D, we reflect in a plane rather than a line:
- is also called the - plane
- is also called the - plane
- is also called the - plane A diagram illustrating the planes is shown below:
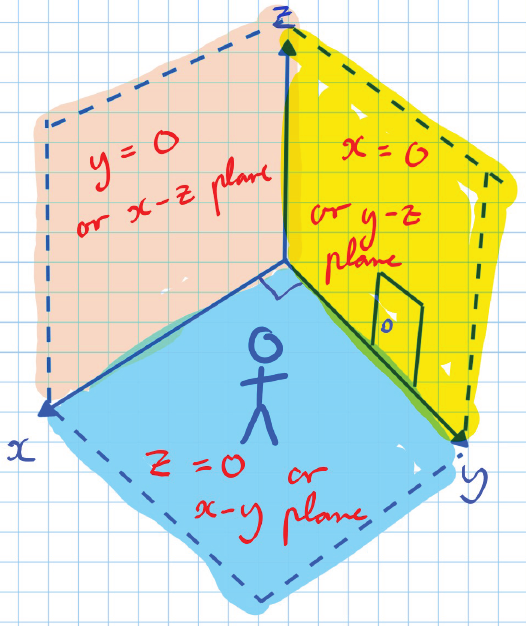
- Red: or - plane
- Yellow: or - plane
- Blue: or - plane
Reflection Matrices
Reflection matrices transform vectors by flipping their coordinates relative to a given plane. The unaffected coordinates remain the same, while the reflected coordinate changes sign.
Reflection in the plane
Here, only the s change, while the and coordinates remain unchanged.
For example:
The reflection matrix for this transformation is:
Reflection Matrices for Other Planes
Reflection in the plane:
Here, only the changes sign.
Reflection in the plane:
Only the changes sign.
Example: Reflect the vector
in the plane.
Step 1**:** Use the reflection matrix :
Step 2**:** Multiply the matrix by the vector :
Step 3**:** Perform the matrix-vector multiplication:
The reflected vector is
Rotation Matrices
Rotation matrices describe transformations where a vector is rotated about a specific axis by an angle .
Rotation About the
Rotation About the
Rotation About the
Example: Rotate the vector
by about the .
Step 1: Use the rotation matrix for rotation. For :
Step 2: Multiply by the vector :
Step 3: Perform the matrix-vector multiplication:
The rotated vector is
which shows a counterclockwise rotation about the
500K+ Students Use These Powerful Tools to Master Matrix Dimensions For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Matrix Dimensions
Revise key concepts with interactive flashcards.
Try Further Maths Core Pure Flashcards5 quizzes
Quizzes on Matrix Dimensions
Test your knowledge with fun and engaging quizzes.
Try Further Maths Core Pure Quizzes29 questions
Exam questions on Matrix Dimensions
Boost your confidence with real exam questions.
Try Further Maths Core Pure Questions27 exams created
Exam Builder on Matrix Dimensions
Create custom exams across topics for better practice!
Try Further Maths Core Pure exam builder50 papers
Past Papers on Matrix Dimensions
Practice past papers to reinforce exam experience.
Try Further Maths Core Pure Past PapersOther Revision Notes related to Matrix Dimensions you should explore
Discover More Revision Notes Related to Matrix Dimensions to Deepen Your Understanding and Improve Your Mastery
