16.1.2 Continuous Random Variables

Continuous Random Variables

Discrete random variables can only take discrete values.
- Example: $X \sim B(3, 0.25), X \in \{0, 1, 2, 3\}$
- $P(X = 1.5)$ does not make sense.
Continuous random variables can take values across a continuous scale, allowing us to model real-life occurrences such as heights of trees, masses of babies, etc.

Functions of Continuous Random Variables

Given the probability density function of a continuous random variable $X$ , it is possible to find the probability density function or cumulative distribution function of $F(X)$ where $F$ is any function.

Worked Example

lightbulbExample

Example $X$ is a random variable that represents the length of the side of a square. The length of the side of the square is equally likely to take any value between 1 and 3.

Find the cumulative distribution function for the area of the square $A$ and hence its probability density function.

Step 1: Define the probability density function for the given variable:

f(x) = \begin{cases} \frac{1}{2} & \text{for } 1 \leq x \leq 3 \\ 0 & \text{otherwise} \end{cases}

Step 2: Determine the cumulative distribution function for this variable:

F(x) = \int_1^x \frac{1}{2} \, dx = \left[ \frac{1}{2}x \right]_1^x = \frac{1}{2}x - \frac{1}{2}

Thus:

F(x) = \begin{cases} 0, & x < 1 \\ \frac{1}{2}x - \frac{1}{2}, & 1 \leq x \leq 3 \\ 1, & x > 3 \end{cases}

Step 3: State the relationship between the two variables:

$X$ = length of the side of the square.
$A$ = area of the square. Thus:

A = X^2

Step 4: Define the cumulative distribution function ( $CDF$ ) of the target distribution in terms of probabilities:

$G(a) = P(A \leq a)$

Using $G$ to define the $CDF$ of $A$ .

Step 5: Rewrite the above cumulative distribution function in terms of the original variable. This rearranges to make the original variable the subject:

G(a) = P(X^2 \leq a) = P(-\sqrt{a} \leq X \leq \sqrt{a})

At this point, check whether the two limits make sense. In this case, $X$ can only take values between 1 and 3 from its initial definition.

= P(1 \leq X \leq \sqrt{a}) \quad \text{(This is G(A))}.

Step 6: Evaluate the probability using the original cumulative distribution function:

P(1 \leq X \leq \sqrt{a}) = F(\sqrt{a}) - F(1)

= \frac{{1}}{2}\sqrt a - \frac{1}{2} - 0 = \frac{1}{2} \sqrt{a} - \frac{1}{2}

(Remember to state the domain):

G(a) = \begin{cases} 0 & a < 1 \\ \frac{1}{2} \sqrt{a} - \frac{1}{2} & 1 \leq a \leq 9 \quad (\text{since } 1 \leq x \leq 3 \text{ and } A = X^2) \\ 1 & a > 9 \end{cases}

Step 7: If asked to find the probability density function, we find that $G'(A) = g(A)$ :

g(a) = G'(a) = \frac{d}{da} \left( \frac{1}{2} a^{\frac{1}{2}} - \frac{1}{2} \right) = \frac{1}{4} a^{-\frac{1}{2}}

Thus:

g(a) = \begin{cases} \frac{1}{4} a^{-\frac{1}{2}} & 1 \leq a \leq 9 \\ 0 & \text{otherwise} \end{cases}

infoNote

Past Paper Example

Q4 (June 2010, Q8)

The continuous random variable $S$ has a probability density function given by:

f(s) = \begin{cases} \frac{8}{3s^{-3}} & 1 \leq s \leq 2 \\ 0 & \text{otherwise} \end{cases}

An isosceles triangle has equal sides of length $S$ , and the angle between them is 30°. (See diagram.)

(i) Find the (cumulative) distribution function of the area $X$ of the triangle, and hence show that the probability density function of $X$ is $\frac{1}{3x^2}$ over an interval to be stated.

(ii) Find the median value of $X$ .

Solution: i)

f(s) = \frac{8}{3} s^{-3} \quad \Rightarrow \quad F(s) = \int_1^s \frac{8}{3} s^{-3} \, ds = \left[ -\frac{4}{3} s^{-2} \right]_1^s

= -\frac{4}{3} s^{-2} + \frac{4}{3} = \frac{4}{3} - \frac{4}{3} s^{-2}

Thus:

F(s) = \begin{cases} 0 & s < 1 \\ \frac{4}{3} - \frac{4}{3} s^{-2} & 1 \leq s \leq 2 \\ 1 & s > 2 \end{cases}

The area of the triangle is given by:

X = \frac{1}{2} S^2 \sin 30^\circ = \frac{1}{4} S^2

Thus:

G(x) = P(X \leq x) = P\left( \frac{1}{4} S^2 \leq x \right)

= P(S^2 \leq 4x) = P(-2\sqrt{x} \leq S \leq 2\sqrt{x})

= P(1 \leq S \leq 2\sqrt{x}) \quad \text{since} \quad 1 \leq S \leq 2

\Rightarrow G(x) = F(2\sqrt{x}) - \cancel{F(1)}

= \frac{4}{3} - \frac{4}{3}(2\sqrt{x})^{-2} = \frac{4}{3} - \frac{\cancel{4}}{3} \times \frac{1}{\cancel 4x} = \frac{4}{3} - \frac{1}{3x}

Thus:

G(x) = \begin{cases} 0 & x < \frac{1}{4} \\ \frac{4}{3} - \frac{1}{3x} & \frac{1}{4} \leq x \leq 1 \\ 1 & x > 1 \end{cases}

From the given diagram, we note that $1 \leq S \leq 2$ and $x = \frac{1}{4} S^2$ .

Thus:

G(x) = \frac{4}{3} - \frac{1}{3}x^{-1} \Rightarrow G'(x) = \frac{1}{3}x^{-2}=\frac {1}{3x^2} \quad (\text{as required})

Thus:

g(x) = \begin{cases} \frac {1}{3x^2} & \frac{1}{4} \leq x \leq 1 \\ 0 & \text{otherwise} \end{cases}

Solution: (ii) Find the median value of $x$ .

The median is $x$ such that $G(x) = 0.5$ :

\frac{4}{3} - \frac{1}{3x} = 0.5 \quad \Rightarrow \quad -\frac{1}{3x} = -\frac{5}{6} \quad \Rightarrow \quad 1 = \frac{15x}{6}

Thus:

x = \frac{6}{15} = \frac{2}{5} \quad \Rightarrow \text{Median is} \quad \frac{2}{5}

Mean and Variance of Continuous Random Variables (CRVs)

infoNote

Recap of Mean and Variance of Discrete Random Variables:

$\text{Mean} = E(X) = \sum x p$

$\text{Variance} = E(X^2) - E(X)^2 = \sum x^2 p - \left( \sum x p \right)^2$

For CRVs, the concept of mean and variance does not change.

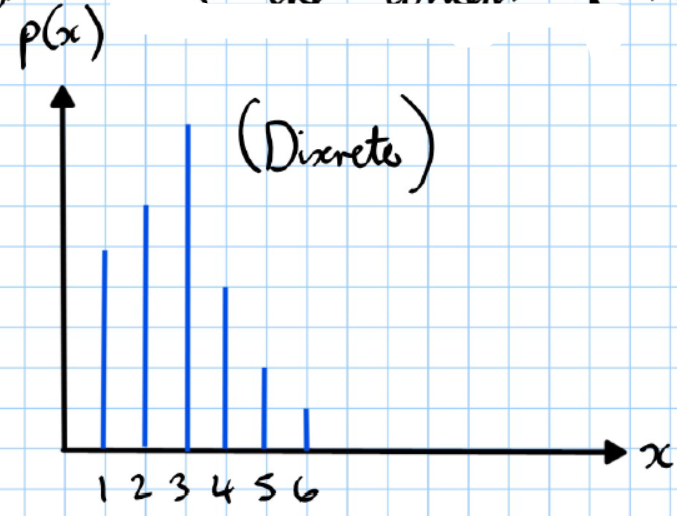
To calculate E(X) , we take all the x values multiplied by the corresponding p -values, then calculate the sum.

As the number of strips becomes infinite, $\sum x p(x)$ becomes $\int x p(x) dx .$

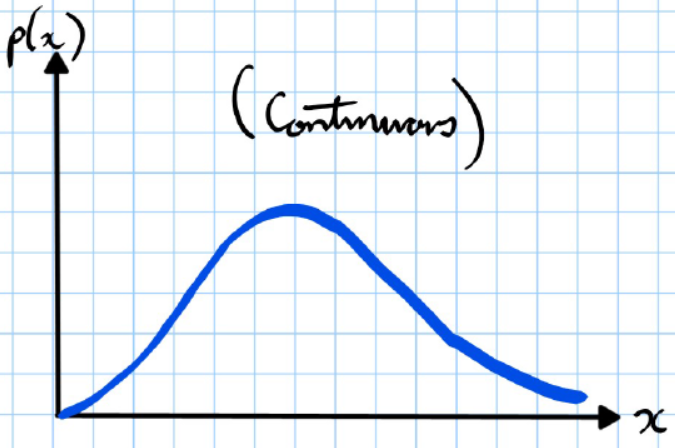
For CRVs:

$E(X) = \int x p(x) dx$

$E(X^2) = \int x^2 p(x) dx$

$\text{Var}(X) = E(X^2) - E(X)^2$

Where p(x) is the probability density function.

infoNote

Worked Example

a) $E(Y) = \int_0^4 y f(y) dy = \int_0^4 y \frac{y}{8} dy = \frac{1}{8} \int_0^4 y^2 dy = \frac{[y^3/3]}{8} \Bigg|_0^4$

$= \frac{4^3}{24} = \frac{64}{24} = \frac{8}{3}$

b) $\text{Var}(Y) = E(Y^2) - E(Y)^2$

$E(Y^2) = \int_0^4 y^2 f(y) dy = \frac{1}{8} \int_0^4 y^3 dy = \frac{[y^4/4]}{8} \Bigg|_0^4 = \frac{4^4}{32} = \frac{256}{32} = 8$

$\text{Var}(Y) = 8 - \left(\frac{8}{3}\right)^2 = 8 - \frac{64}{9} = \frac{72}{9} - \frac{64}{9} = \frac{8}{9}$

c) Remember: $\sigma = \sqrt{\text{Variance}}$

$\sigma = \sqrt{\frac{8}{9}} = \frac{2\sqrt{2}}{3}$

d) $P(Y > \mu)$

$P(Y > \frac{8}{3}) = \int_{8/3}^4 \frac{y}{8} dy = \frac{1}{16} \Bigg[ y^2 \Bigg|_{8/3}^4 \Bigg] = \frac{4^2}{16} - \left(\frac{8}{3}\right)^2$

$= \frac{16}{16} - \frac{64}{9 \times 16} = \frac{5}{9}$

e) $\text{Var}(3Y + 2) = 3^2 \times \text{Var}(Y) = 9 \times \frac{8}{9} = 8$

f) $E(Y + 2) = \frac{8}{3} + 2 = \frac{14}{3}$

Remember:

$\text{Var}(aX + b) = a^2 \text{Var}(X), \quad E(aX + b) = aE(X) + b$

Median, Mode, and Skewness of CRV

Mode

The mode of a continuous random variable (CRV) is the maximum of its probability density function (if a maximum exists).

lightbulbExample

Example The continuous random variable $X$ has a probability density function given by:

f(x) = \begin{cases} \frac{3}{80} (8 + 2x - x^2) & \text{for } 0 \leq x \leq 4, \\ 0 & \text{otherwise.} \end{cases}

Tasks

a) Sketch the probability density function of $X$ .

b) Find the mode of $X$ .

a) $f(x) = \frac{3}{80}(x^2 - 2x - 8) = \frac{-3}{80}(x - 4)(x + 2)$

                                      (Root at $ x = 4$  or  $x = -2$

$f(0) = \frac{-3}{80}(8) = \frac{3}{10}$

LHS (left-hand side) is in $(0, \frac{3}{10})$ .

$f(4) = \frac{-3}{80}(4^2 - 2(4) - 8) = 0$

RHS (right-hand side) is $(4, 0)$ .

b) The mode may or may not be a local maximum as found by differentiation.

In this P.D.F., differentiating and finding the stationary point would lead to a mode outside of the domain of validity of the P.D.F. Here, from observing where the function is valid, we see the mode is f(0) .

(In this question, the mode is found by differentiation.)

$f(x) = \frac{3}{80} (8 + 2x - x^2) \quad 0 \leq x \leq 4 \quad \text{otherwise}$

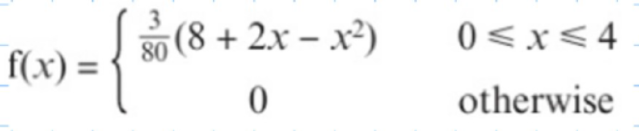
(i.e., mode on this function is the stationary point)

$f'(x) = \frac{3}{80} (2 - 2x) = 0$

$\Rightarrow 2 = 2x \Rightarrow x = 1$

Mode = $x -value$ point with the highest frequency.

:::

Median

The median is the value of $x$ to the left of which 0.5 of the probability lies and to the right of which 0.5 of the probability lies.

Method 1: Using P.D.F.

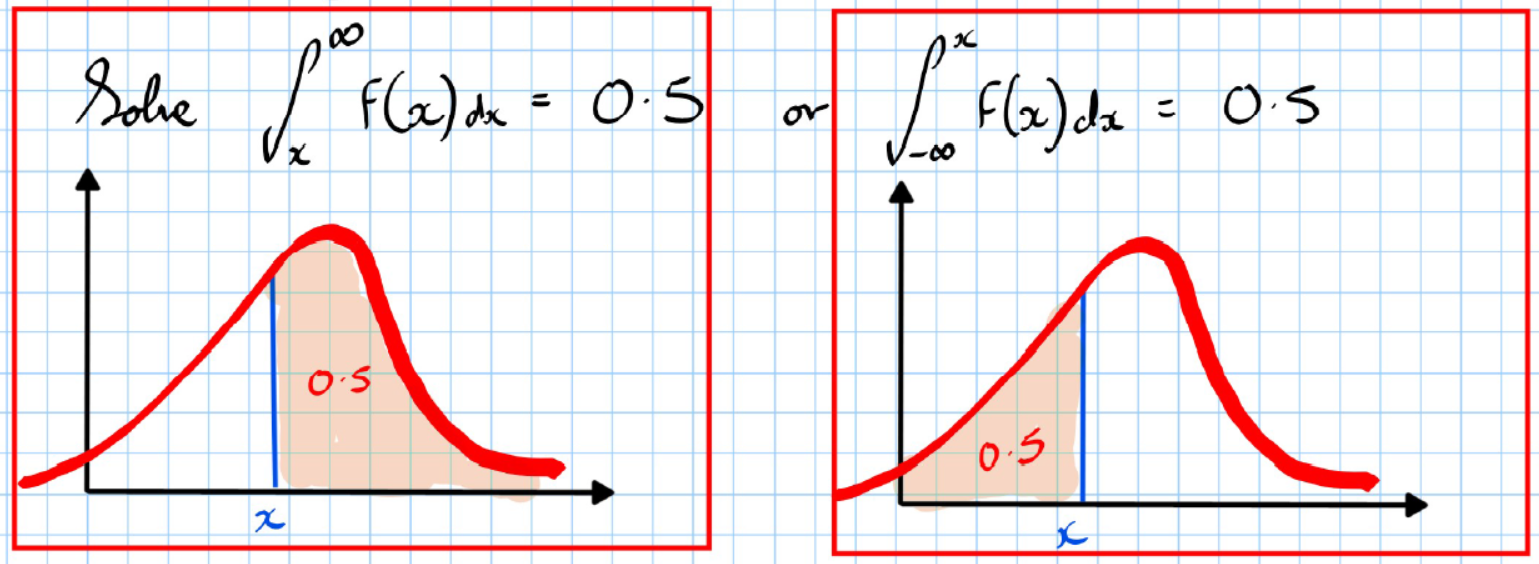
Method 2: Use C.D.F.

Solve $F(x) = 0.5$

lightbulbExample

Example: The continuous random variable $X$ has a cumulative distribution function given by:

F(x) = \begin{cases} 0 & x < 0, \\ \frac{x^2}{6} & 0 \leq x \leq 2, \\ -\frac{x^2}{3} + 2x - 2 & 2 \leq x \leq 3, \\ 1 & x > 3. \end{cases}

Tasks

a) Find the median value of $X$ .

b) Find the quartiles and the interquartile range (IQR) of $X$ .

Note: Ensure answers are given to 3 decimal places.

a) $F(x) = 0.5$

$0.5 = \frac{x^2}{6} \Rightarrow x^2 = 3 \Rightarrow x = \sqrt{3}$

(Since $\sqrt{3} \approx 1.732$ and $0 \leq x \leq 2$ , this is valid.)

b) $F(x) = 0.75$ (Upper quartile)

$0.75 = \frac{x^2}{6} \Rightarrow x^2 = 4.5 \Rightarrow x = \frac{3\sqrt{2}}{2}$

(But this is not valid, so we use the second part of the function.)

$F(x) = \frac{-x^3}{3} + 2x - 2 = 0.75$

$\Rightarrow -\frac{x^3}{3} + 2x - 2.75 = 0 \Rightarrow x = \frac{6 - \sqrt{13}}{2} \approx 2.154$

Thus, $\text{UQ} = \frac{6 - \sqrt{13}}{2} \approx 2.154 .$

$LQ:$ $F(x) = 0.25$

$0.25 = \frac{x^2}{6} \Rightarrow x^2 = \frac{3}{2} \Rightarrow x = \frac{\sqrt{6}}{2} \approx 1.225$

Thus, $\text{LQ} = \frac{\sqrt{6}}{2} \approx 1.225$

Interquartile Range (IQR):

$IQR = \frac{6 - \sqrt{3}}{2} - \frac{\sqrt{6}}{2} \approx 0.909$

Continuous Random Variables Simplified Revision Notes for A-Level Edexcel Further Maths Further Statistics 1

16.1.2 Continuous Random Variables

Continuous Random Variables

Functions of Continuous Random Variables

Worked Example

Past Paper Example

Mean and Variance of Continuous Random Variables (CRVs)

Worked Example

Median, Mode, and Skewness of CRV

Mode

Median

500K+ Students Use These Powerful Tools to Master Continuous Random Variables For their A-Level Exams.

Other Revision Notes related to Continuous Random Variables you should explore