2.1.2 Velocity-Time Graphs

V-T and S-T Graphs

A ball is bouncing on the ground. It is released from a height of 1 m above the ground.

S-T Graph

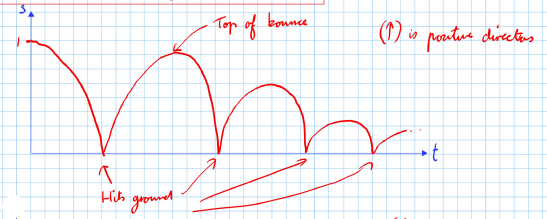
Assumptions:

• The ground is s = 0.
• g is positive direction (acceleration due to gravity).

Graph Explanation:

• The graph shows a series of parabolic curves representing the motion of the ball as it bounces.
• The ball hits the ground and then changes direction at the moment of bounce.
• Each bounce reaches a lower height until the ball eventually stops.

V-T Graph

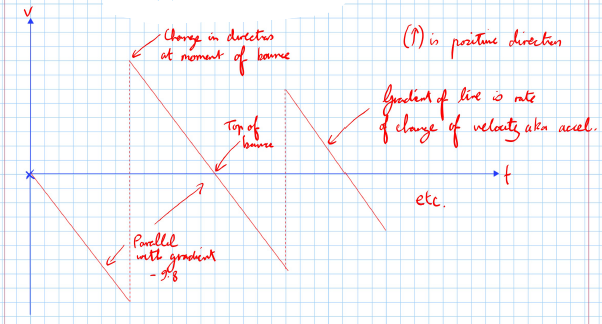
• g is positive direction (acceleration due to gravity).
• The graph shows a series of straight lines with negative slopes, indicating the decrease in velocity as the ball moves upwards and increases in the downward direction.
• The gradient of the line represents the rate of change of velocity, also known as acceleration.
• The velocity reaches zero at the top of each bounce before reversing direction.
• The lines are parallel, with a gradient of -9.8 m/s², showing constant acceleration due to gravity during the ball's motion.

Features of an S-T Graph

• At time t = 6, the displacement is 10 m.
• At t = 6 ≤ t ≤ 20, the particle does not displace itself further; it is at rest.
• At t = 24, the particle has displacement 0 m.
• During this fascinating episode, the particle has travelled a distance of 20 m.

1. For 0 ≤ t ≤ 6:

• Its velocity is ΔS/Δt = 10/6 = 5/3 ms⁻¹.

2. For 20 ≤ t ≤ 24:

• Its velocity is ΔS/Δt = -10/4 = -2.5 ms⁻¹.

3. For 20 ≤ t ≤ 24:

• Its speed is 2.5 ms⁻¹.

4. For 0 ≤ t ≤ 24:

• Its average velocity is ΔS/Δt = 0/24 = 0 ms⁻¹.

5. For 0 ≤ t ≤ 24:

• Its average speed is 20/24 = 5/6 ms⁻¹.

Key Points

---

Features of a V-T Graph

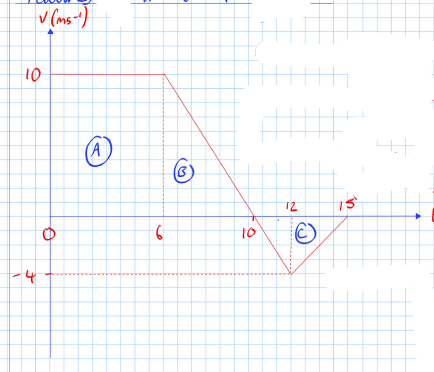
6. For 0 ≤ t ≤ 6:

• Moving at a constant velocity of 10 ms⁻¹.

7. For 6 ≤ t ≤ 10:

• Velocity decreases at a constant rate of ΔV/Δt = (10 - 2)/4 = 2 ms⁻².

8. For 10 ≤ t ≤ 12:

• Change in direction with decrease in velocity/increase in speed.

9. For 12 ≤ t ≤ 15:

• Decrease in speed but accelerating positively at a rate of 4/3 ms⁻².

Total Displacement Calculation

The total displacement is the sum of all the individual areas between the graph and the x-axis, including their signs.

• Total displacement from 0 ≤ t ≤ 15:
  • A = 6 × 10 = 60 m
  • B = (10 × 4)/2 = 20 m
  • C = (5 × -4)/2 = -10 m
  • Total displacement: 60 + 20 - 10 = 70 m
  • Total distance travelled: 60 + 20 + 10 = 90 m

Key Points