3.1.3 Equilibrium in 2D

infoNote

To approach equilibrium questions in 2D Mechanics, follow these key steps:

Identify all forces: List all the forces acting on the object, including weight, tension, normal reaction, and friction.
Resolve forces into components: Split each force into horizontal and vertical components, typically using trigonometry (sine and cosine functions for angled forces).
Apply equilibrium conditions: For an object in equilibrium, the sum of forces in both directions must equal zero:

$\sum F_x = 0$ (sum of horizontal forces)
$\sum F_y = 0$ (sum of vertical forces)

Solve the system of equations: Use the two equations to find unknown forces or angles. This method ensures that all forces balance, confirming that the object is in equilibrium.

Static Bodies in 2D

Concept:

A static body is an object that lies in equilibrium. In this scenario, all forces attached to the object sum to zero.

infoNote

Example:

Consider a scenario where a single piece of string is threaded through a particle, with the string being light and inextensible. The particle is held in equilibrium by two strings forming angles of $30^\circ$ with the horizontal. Problem:
Given that the weight of the particle is $2$ g, find the tension $T$ in the strings. Solution:

Resolve Forces in a Relevant Direction:

Consider the vertical direction for resolving forces.

Vertical Forces:

T \sin 30^\circ + T \sin 30^\circ - 2g = 0

Since $\sin 30^\circ = \frac{1}{2}$ , the equation simplifies to:

2T \cdot \frac{1}{2} - 2g = 0

T - 2g = 0 \quad \Rightarrow \quad T = 2g \, \text{N}

Final Answer:

The tension in each string is $T = 2g \, \text{N}$ .

Mechanics Problems in 3D

Key Concept:

All mechanical concepts (equilibrium, $F = ma$ , SUVAT, etc.) apply in 3D as well as in 2D.

infoNote

Q1, (Jan 2005, Q3)

Problem Statement: A particle is in equilibrium when acted on by the forces $\left(\begin{array}{c} x \\ -7 \\ z \end{array}\right), \left(\begin{array}{c} 4 \\ y \\ -5 \end{array}\right), and \left(\begin{array}{c} 5 \\ 4 \\ -7 \end{array}\right)$ , where the units are Newtons.

Find the values of $x$ , $y$ , and $z.$
Calculate the magnitude of $\left(\begin{array}{c} 5 \\ 4 \\ -7 \end{array}\right)$ .

Solution:

Part (i): Finding the Values of $x$ , $y$ , and $z$

Condition for Equilibrium:

Since the particle is in equilibrium, the sum of all forces must be zero:

\left(\begin{array}{c} x \\ -7 \\ z \end{array}\right) + \left(\begin{array}{c} 4 \\ y \\ -5 \end{array}\right) + \left(\begin{array}{c} 5 \\ 4 \\ -7 \end{array}\right) = \left(\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right)

Solve for $x$ , $y$ , and $z$ :

Equating the components:

x + 4 + 5 = 0 \quad \Rightarrow \quad x = -9

-7 + y + 4 = 0 \quad \Rightarrow \quad y = 3

z - 5 - 7 = 0 \quad \Rightarrow \quad z = 12

Answer (i): $x = -9, y = 3, z = 12$

Part (ii): Calculating the Magnitude

Calculate the magnitude of $\left(\begin{array}{c} 5 \\ 4 \\ -7 \end{array}\right)$ :

|\mathbf{a}| = \sqrt{5^2 + 4^2 + (-7)^2} = \sqrt{25 + 16 + 49} = \sqrt{90} = 3\sqrt{10}

Answer (ii): The magnitude is $3\sqrt{10}$ .

Problem: Finding the Tension in the String and the Weight of the Bead

infoNote

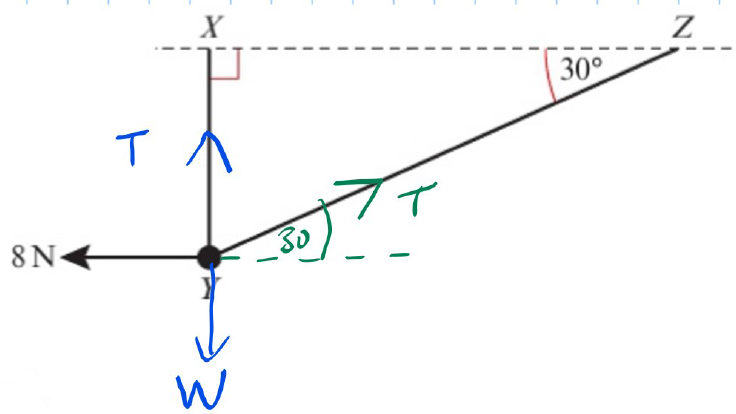
Problem Statement:

A smooth bead Y is threaded on a light inextensible string.
The string is attached to two fixed points, $X$ and $Z$ , which are on the same horizontal level.
The bead is in equilibrium, held by a horizontal force of magnitude $8 \, \text{N}$ acting parallel to $ZX$ .
The bead $Y$ is vertically below $X$ , and \angle $\angle XZY = 30^\circ$ . Find:
The tension in the string $T$ .
The weight of the bead $W$ .

Solution:

Tension $T$ in the String:

Since the bead is in equilibrium and the string is inextensible, the tension is the same throughout the string.
Resolve forces horizontally:

T \cos 30^\circ = 8 \, \text{N}

T = \frac{8}{\cos 30^\circ} = \frac{8}{\frac{\sqrt{3}}{2}} = \frac{16}{\sqrt{3}} \, \text{N} \approx \frac{16\sqrt{3}}{3} \, \text{N}

Weight $W$ of the Bead:

Resolve forces vertically:

T \sin 30^\circ + T \sin 30^\circ = W

W = 2 \times T \sin 30^\circ

W = 2 \times \frac{16\sqrt{3}}{3} \times \frac{1}{2} = \frac{16\sqrt{3}}{3} \, \sin30 ^\circ = \boxed {8\sqrt 3N}

Answer:

Tension $T \approx \frac{16\sqrt{3}}{3} \, \text{N}$
Weight $W \approx 8\sqrt{3} \, \text{N}$

Problem: Tension in the String and Weight of the Bead

infoNote

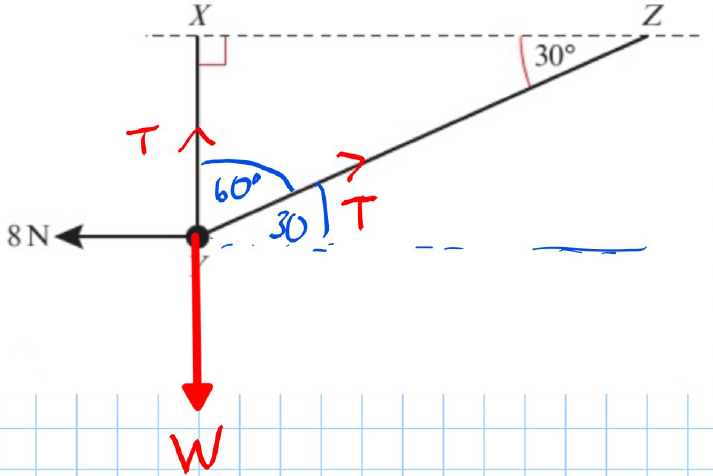
Problem Statement:

A smooth bead $Y$ is threaded on a light inextensible string. The ends of the string are attached to two fixed points, $X$ and $Z$ , on the same horizontal level.
The bead is in equilibrium under a horizontal force of magnitude $8 \, \text{N}$ acting parallel to $ZX$ .
The bead $Y$ is vertically below $X$ , and $\angle ZXY = 30^\circ$ . Objective:
Find the tension $T$ in the string.
Find the weight $W$ of the bead.

Solution:

Resolving Forces Horizontally:

The horizontal component of the tension $T$ must balance the horizontal force:

8 - T \cos 30^\circ = 0

T \cos 30^\circ = 8

T = \frac{8}{\cos 30^\circ} = \frac{8}{\frac{\sqrt{3}}{2}} = \frac{16\sqrt{3}}{3} \, \text{N}

Resolving Forces Vertically:

The vertical components of the tension $T$ must balance the weight $W$ :

T \sin 30^\circ + T \cos 60^\circ - W = 0

Substituting $\sin 30^\circ = \frac{1}{2}$ and $\cos 60^\circ = \frac{1}{2}$ :

T \times \frac{1}{2} + T \times \frac{1}{2} = W

W = \frac{1.5T}{2} = T \sin 30^\circ + T \cos 60^\circ

W = \frac{16\sqrt{3}}{3} \times \frac{3}{2} = 8\sqrt{3} \, \text{N}

Final Answer:

Tension in the string $T$ is $\frac{16\sqrt{3}}{3} \, \text{N}$ .
Weight of the bead $W$ is $8\sqrt{3} \, \text{N}$ .

Equilibrium in 2D Simplified Revision Notes for A-Level Edexcel Maths Mechanics

3.1.3 Equilibrium in 2D

Static Bodies in 2D

Mechanics Problems in 3D

Q1, (Jan 2005, Q3)

Solution:

Part (i): Finding the Values of $x$ , $y$ , and $z$

Part (ii): Calculating the Magnitude

Problem: Finding the Tension in the String and the Weight of the Bead

Solution:

Problem: Tension in the String and Weight of the Bead

Solution:

500K+ Students Use These Powerful Tools to Master Equilibrium in 2D For their A-Level Exams.

Other Revision Notes related to Equilibrium in 2D you should explore

Equilibrium in 2D Simplified Revision Notes for A-Level Edexcel Maths Mechanics

3.1.3 Equilibrium in 2D

Static Bodies in 2D

Mechanics Problems in 3D

Q1, (Jan 2005, Q3)

Solution:

Part (i): Finding the Values of xxx, yyy, and zzz

Part (ii): Calculating the Magnitude

Problem: Finding the Tension in the String and the Weight of the Bead

Solution:

Problem: Tension in the String and Weight of the Bead

Solution:

500K+ Students Use These Powerful Tools to Master Equilibrium in 2D For their A-Level Exams.

Other Revision Notes related to Equilibrium in 2D you should explore

Part (i): Finding the Values of $x$ , $y$ , and $z$