The equation of trajectory describes the path of an object under projectile motion, typically in a parabolic form. It combines both horizontal and vertical components of motion, assuming constant acceleration due to gravity and no air resistance.

For an object launched with initial velocity $u$ at an angle $\theta$ from the horizontal:

• Horizontal displacement ( $x$ ): $x = u \cos(\theta) \cdot t$
• Vertical displacement ( $y$ ): $y = u \sin(\theta) \cdot t - \frac{1}{2} g t^2$ By eliminating time $t$ , the trajectory equation is:

This equation represents a parabola and shows the relationship between horizontal and vertical displacements of the projectile.

Example:

A particle is projected at an angle of $60^\circ$ above the horizontal with an initial speed of $40 ms$. Find the Cartesian equation for the path (trajectory) of the particle.

Steps:

1. Note all initial conditions as vectors in SUVAT.

Given:

• $\mathbf{u} = \left(40\cos60^\circ, 40\sin60^\circ\right)$
• $\mathbf{a} = \left(0, -9.8\right)$
• $\mathbf{s} = ?$
• $t = t$

2. Use $\mathbf{s} = \mathbf{ut} + \frac{1}{2} \mathbf{a}t^2$ to get the parametric equations of motion in terms of $t.$

3. Write the equation in $x$ and $y$ in terms of t, then eliminate t.

Given:

$x = 20t$

$y = 20\sqrt{3}t - 4.9t^2$

Substituting $t = \frac{x}{20}$ into the equation for $y$:

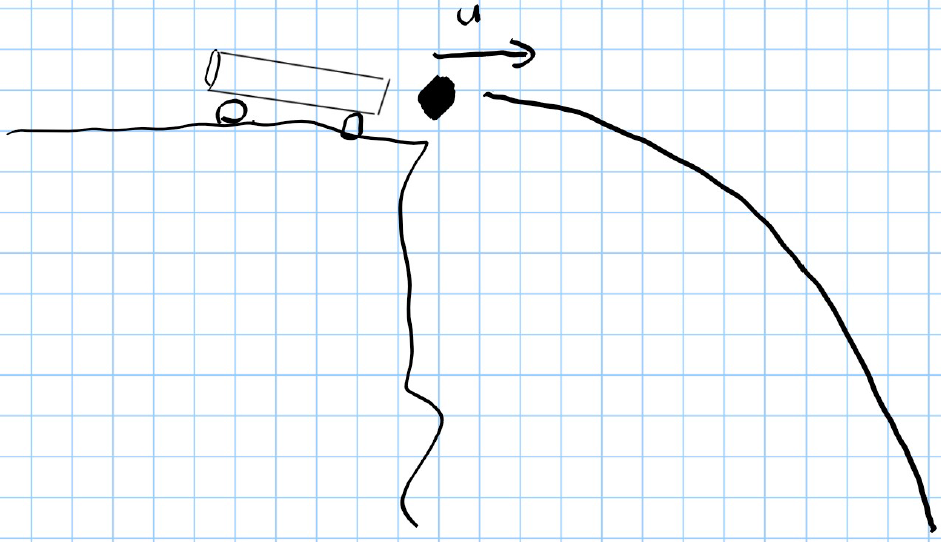
Example:

A particle is projected horizontally at an initial speed of $15 ms^{-1}$. 10 seconds later, it hits the ground. Find the distance above the ground from which it was projected.

Solution:

Given:

• Initial velocity $\mathbf{u} = (15, 0)ms$
• Acceleration $\mathbf{a} = (0, -9.8) ms^2$
• Time $t = 10 s$
• Displacement $\mathbf{s} = ?$

Steps:

1. Set positive directions:

• Positive $x$-direction is rightward (horizontal)
• Positive $y$-direction is upward (vertical)

2. Use the SUVAT equation:

3. Calculate the horizontal displacement x:

4. Calculate the vertical displacement h:

Therefore, the height $h = 490 m$.

Note:

To calculate the total distance from the origin O, use: