3.2.4 Connected Bodies - Pulleys

How to approach pulley questions:

infoNote

Step 1: Break Down the Problem

Start by carefully analysing the problem. You're dealing with two bodies connected by a string that passes over a pulley. The first step is to understand that the string is inextensible (it doesn't stretch), which means both bodies will accelerate at the same rate, but in opposite directions (one up, one down).
Identify the forces acting on each body:
For the body hanging vertically, the main forces are gravity (weight) pulling it down and tension in the string pulling it up.
For the body on a horizontal surface (or another body hanging), consider tension pulling it in one direction and its weight (which might contribute to friction if on a surface) pulling it down.

Step 2: Set Up Equations Using Newton's Second Law

Use Newton's second law $(F = ma)$ to set up equations for each body:
For the hanging body: $mg - T = ma$ , where $m$ is the mass, $g$ is gravity, $T$ is the tension, and $a$ is the acceleration.
For the other body (which could be on a surface or also hanging): $T - mg = ma$ or $T - f = ma$ (where $f$ is friction).
Remember, both bodies share the same tension in the string and have the same acceleration, but the direction of these forces is crucial.

Step 3: Solve the Equations Simultaneously

You now have two equations with two unknowns: the tension $T$ and the acceleration $a$ . Solve these equations simultaneously:
Add or subtract the equations to eliminate one variable and solve for the other.
Once you find $a$ , plug it back into one of the original equations to find $T$ . Step 4: Interpret Your Results
After solving, ensure your results make physical sense:
Check the direction of the acceleration and whether the tension is realistic (e.g., it shouldn't be negative).
Consider edge cases, such as what happens if the masses are equal or if there's no friction.

Problem: Particles over a Pulley

infoNote

Given:

Particles $P$ and $Q$ , of masses 2m and 3m, are attached to the ends of a light inextensible string.
The string passes over a small smooth fixed pulley, and the masses hang with the string taut.
The system is released from rest. Questions:

i) Write down an equation of motion for $P$ . ii) Write down an equation of motion for $Q$ .
Find the acceleration of each mass.
Find the tension in the string.

Solution:

Step 1: Draw a Diagram

$T$ is the tension in the string.
$P$ experiences a downward force of $2mg.$
$Q$ experiences a downward force of $3mg$ .

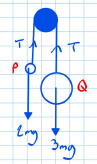
Step 2: Write the Equations of Motion

For Particle $P$ :

Taking the downward direction as positive for $P$ :

T - 2mg = 2ma \quad \text{(Equation 1)}

For Particle Q:

Taking the upward direction as positive for $Q$ :

3mg - T = 3ma \quad \text{(Equation 2)}

Step 3: Solve the Equations Simultaneously

Add Equation $1$ and Equation $2$ to eliminate $T$ :

T - 2mg + 3mg - T = 2ma + 3ma

mg = 5ma

a = \frac{g}{5} \approx :highlight[1.96] \, \text{m/s}^2

Substitute a back into Equation $1$ or $2$ to find $T$ : Using Equation 1:

T - 2mg = 2m \times 1.96

T = 2mg + 3.92m = :highlight[23.52m] \, \text{N}

Final Answers:

Acceleration of each mass: $a = :success[1.96] \, \text{m/s}^2$
Tension in the string: $T = :success[23.52m] \, \text{N}$

Problem: Scale-Pan with Two Masses

infoNote

Given:

A light scale-pan is attached to a vertical light inextensible string.
The scale-pan carries two masses $A$ and $B$ .
Mass of $A = :highlight[400 g]$ and mass of $B = :highlight[600 g]$ .
The scale-pan is raised vertically using the string, with acceleration 0.5 $\, \text{ms}^{-2}$ .

Questions:

Find the tension in the string.
Find the force exerted on mass $B$ by mass $A$ .
Find the force exerted on mass $B$ by the scale-pan.

Solution:

Part (a): Find the Tension in the String

Draw a diagram:

Consider the forces acting on the entire system from the string's point of view.

Apply Newton's Second Law:

$T - (m_A + m_B)g = (m_A + m_B)a$
Convert masses to kilograms: $m_A = :highlight[0.4] \, \text{kg}, m_B = :highlight[0.6] \, \text{kg}$
Total mass: $1 \, \text{kg}$
Gravitational acceleration: $g = 9.8 \, \text{m/s}^2$
Acceleration: $a = 0.5 \, \text{m/s}^2$

Calculate the tension $T$ :

T - 9.8 = 1 \times 0.5

T = 0.5 + 9.8 = :highlight[10.3] \, \text{N}

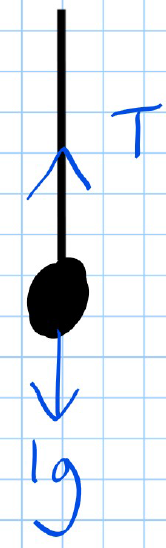
Answer (a): The tension in the string is 10.3 N.

Part (b): Find the Force Exerted on Mass B by Mass A

Consider $A$ as the focus:

A exerts a force on $B$ due to its weight and the acceleration of the system.

Calculate the force using Newton's Second Law:

B = m_A a + m_A g

B = 0.4 \times 0.5 + 0.4 \times 9.8 = :highlight[4.12] \, \text{N}

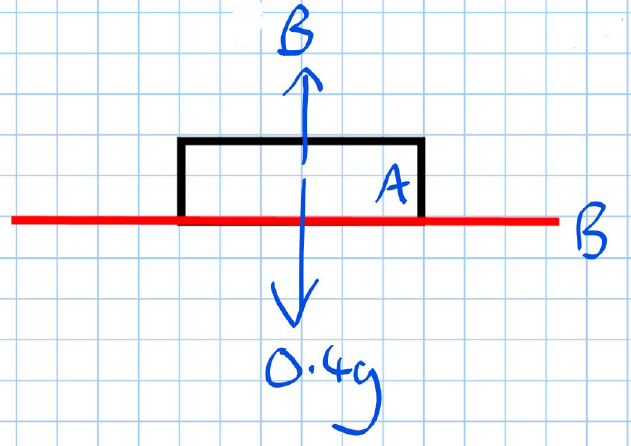
Answer (b): The force exerted on mass B by mass A is 4.12 N.

Part (c): Find the Force Exerted on Mass B by the Scale-Pan

Consider $B$ as the focus:

$B$ is subjected to the tension force from the string and the reaction force from $A$ .

Calculate the force using Newton's Second Law:

P - m_B a - m_B g = 0

P = m_B (g + a) = 0.6 \times (9.8 + 0.5) = :highlight[10.2] \, \text{N}

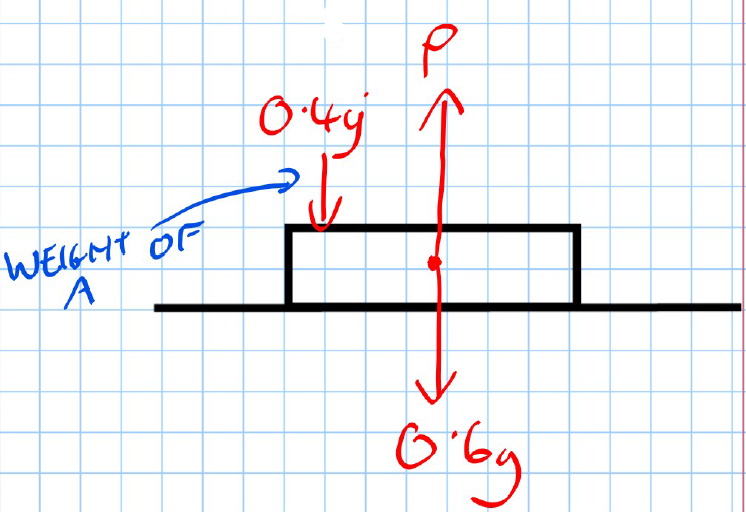
Answer (c): The force exerted on mass $B$ by the scale-pan is 10.2 N.

Problem: Calculating Forces on a Mass on an Inclined Plane with a Pulley

infoNote

Problem Statement:

A mass of 3 kg rests on a smooth plane inclined at 45° to the horizontal.
The mass is attached to a cable that passes up the plane along the line of the greatest slope and over a smooth pulley at the top of the plane.
The other end of the cable carries a mass of 1 kg freely suspended.
A horizontal force P acts on the 3 kg mass, and the system is in equilibrium.

Calculate:

The magnitude of P.
The normal reaction R between the mass and the plane.
State how the assumption that the pulley is smooth has been used in your calculations.

Solution:

Part (a): Calculate the Magnitude of $P$

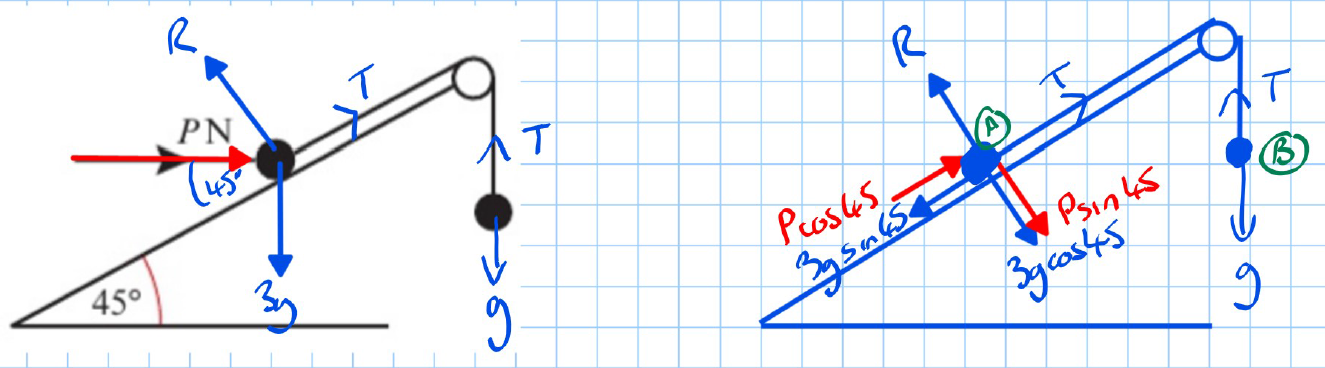
Forces Acting:

Tension $T$ in the string is the same on both sides due to the smooth pulley.
The weight of the 1 kg mass exerts a downward force of $1$ g (where g is the acceleration due to gravity).
The 3 kg mass has components of weight along and perpendicular to the plane.

For the 1 kg mass:

T = 1g \, \text{N}

For the 3 kg mass on the slope:

Resolve forces parallel to the plane:

T + P \cos 45^\circ = 3g \sin 45^\circ

Substituting $T = 1g$ and $\sin 45^\circ = \cos 45^\circ = \frac{\sqrt{2}}{2}$ :

g + P \cdot \frac{\sqrt{2}}{2} = 3g \cdot \frac{\sqrt{2}}{2}

Simplifying:

P = :highlight[2g] \, \text{N} = :highlight[15.541] N

Answer (a): $P = :success[15.541N]$

Part (b): Calculate the Normal Reaction R

Resolve forces perpendicular to the plane:

R = 3g \cos 45^\circ = 3g \cdot \frac{\sqrt{2}}{2} = \frac{3\sqrt{2}}{2}g \, \text{N}=:highlight[31.78]N

Answer (b): $R = :success[31.7N]$

Part (c): Assumption About the Smooth Pulley

The assumption that the pulley is smooth implies that the tension $T$ is the same on both sides of the pulley. This allows us to equate the tension in the string acting on the 1 kg mass to the tension acting on the 3 kg mass, simplifying the calculations. Answer (c): The smooth pulley ensures that the tension in the string is equal on both sides, allowing for straightforward calculations of forces acting on the system.

Tips:

infoNote

Draw free body diagrams: Create separate free body diagrams for each object, showing forces like tension in the rope, weight, and any other forces acting on the bodies.
Apply $F = ma$ for each object: Write separate $F = ma$ equations for each mass. Keep in mind that the acceleration of connected bodies is the same magnitude, but may have different directions (e.g., one object moves up while the other moves down).
Consider the pulley system: The tension in the rope is the same throughout if the pulley is ideal (massless and frictionless). For systems with multiple pulleys, take care to track the relationship between displacements and accelerations of the different masses.

Connected Bodies - Pulleys Simplified Revision Notes for A-Level OCR Maths Mechanics

3.2.4 Connected Bodies - Pulleys

How to approach pulley questions:

Problem: Particles over a Pulley

Solution:

Step 1: Draw a Diagram

Step 2: Write the Equations of Motion

Step 3: Solve the Equations Simultaneously

Final Answers:

Problem: Scale-Pan with Two Masses

Solution:

Part (a): Find the Tension in the String

Part (b): Find the Force Exerted on Mass B by Mass A

Part (c): Find the Force Exerted on Mass B by the Scale-Pan

Problem: Calculating Forces on a Mass on an Inclined Plane with a Pulley

Solution:

Part (a): Calculate the Magnitude of $P$

Part (b): Calculate the Normal Reaction R

Part (c): Assumption About the Smooth Pulley

Tips:

500K+ Students Use These Powerful Tools to Master Connected Bodies - Pulleys For their A-Level Exams.

Other Revision Notes related to Connected Bodies - Pulleys you should explore

Connected Bodies - Pulleys Simplified Revision Notes for A-Level OCR Maths Mechanics

3.2.4 Connected Bodies - Pulleys

How to approach pulley questions:

Problem: Particles over a Pulley

Solution:

Step 1: Draw a Diagram

Step 2: Write the Equations of Motion

Step 3: Solve the Equations Simultaneously

Final Answers:

Problem: Scale-Pan with Two Masses

Solution:

Part (a): Find the Tension in the String

Part (b): Find the Force Exerted on Mass B by Mass A

Part (c): Find the Force Exerted on Mass B by the Scale-Pan

Problem: Calculating Forces on a Mass on an Inclined Plane with a Pulley

Solution:

Part (a): Calculate the Magnitude of PPP

Part (b): Calculate the Normal Reaction R

Part (c): Assumption About the Smooth Pulley

Tips:

500K+ Students Use These Powerful Tools to Master Connected Bodies - Pulleys For their A-Level Exams.

Other Revision Notes related to Connected Bodies - Pulleys you should explore

Part (a): Calculate the Magnitude of $P$