4.1.1 Moments Diagrams

Moments

A moment is the turning effect that a force has. For example, consider a force applied to the following see-saw:

infoNote

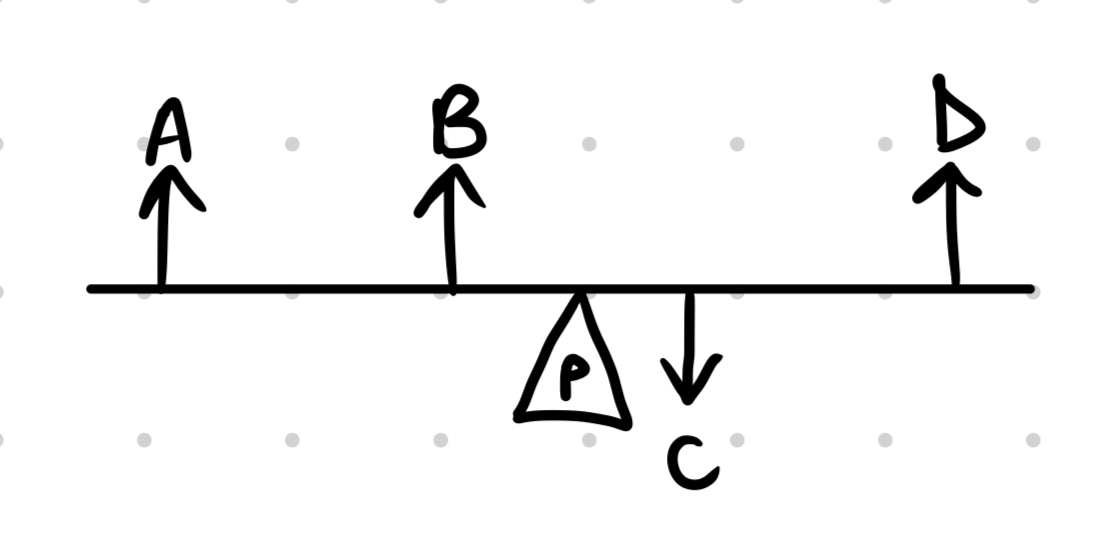
We can see that the see-saw is pivoted about $P$ . Each of the forces $A, B, C$ , and $D$ will have a turning effect (except one). When taking moments about $P$ , considering $P$ to be the pivot and considering clockwise as the positive direction:

Force A has a clockwise moment.
Force B has no turning effect as it is acting into the pivot.
Force C has a clockwise turning effect.
Force D has an anticlockwise turning effect. The magnitude of the moment (or turning effect) of a force is given by:

\text{Moment} = \text{Force} \times \text{Distance}

infoNote

💡Note: The distance refers to the perpendicular distance from the pivot to the line of action of the force.

Problem 1: Jack and Jill on a Seesaw

infoNote

📝Given:

Jack and Jill are playing on a seesaw made from a uniform plank $AB$ of length 5 m, pivoted at $M$ , the midpoint of $AB.$
Jack has a mass of 35 kg and Jill has a mass of 28 kg.
Jill sits at A and Jack sits at a distance x m from $B$ .
The plank is in equilibrium. Find: The value of $x$ .

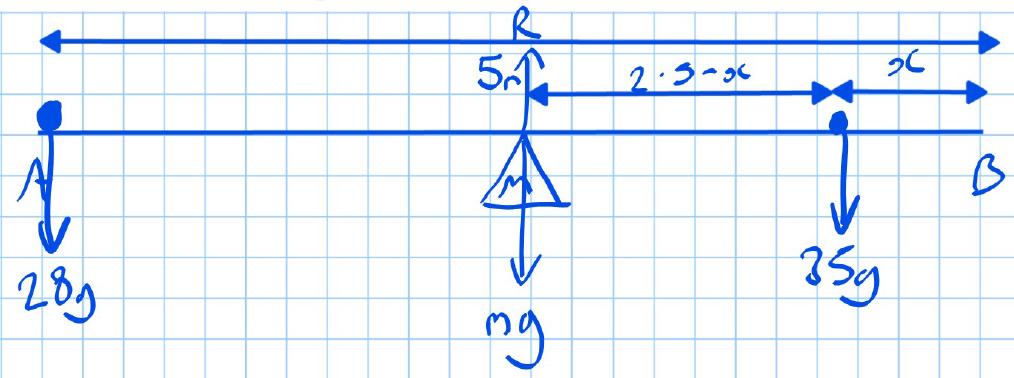
Solution:

Identify the forces and moments:

Weight of Jill = $28g$ acting at $A$ .
Weight of Jack = $35$ g acting at a distance $x$ m from $B$ .
Weight of the plank = mg acting at the centre $M$ (This weight does not cause any turning effect as it acts at the pivot).

Taking moments about the pivot M:

$35g(2.5 - x) - 28g(2.5) = 0$

Solve for $x$ :

35g(2.5 - x) = 70g

2.5 - x = 2 \Rightarrow x = 0.5 \text{ m}

Result: The value of x = 0.5 m.

Problem 2: Q5, (Jan 2010, Q4) Tension in the Rope

infoNote

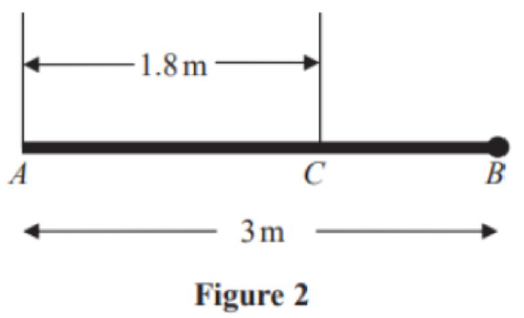
Given:

A pole $AB$ has length 3 m and weight $W$ Newtons.
The pole is held in a horizontal position in equilibrium by two vertical ropes attached at points $A$ and $C$ .
AC = 1.8 m, and a load of weight 20 N is attached to the rod at B.
The pole is modelled as a uniform rod. Find:
(a) The tension in the rope attached to the pole at C in terms of W. $\left (\dfrac {5}{6}W+\dfrac {100}{3} \right)N$
(b) The tension in the rope attached to the pole at $A$ in terms of $W$ .
(c) The value of $W$ given that the tension in the rope at $C$ is eight times the tension in the rope at $A$ .

Solution (a):

Identify the forces and moments:

Let $T_C$ be the tension at $C$ and $T_A$ be the tension at $A$ .
Weight of the pole W acts at the centre of the rod.
The $20$ N force acts at $B$ .

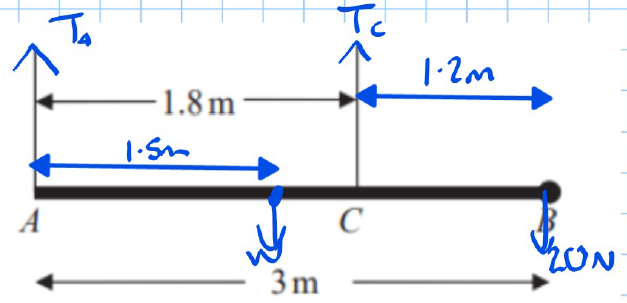
Taking moments about $A$ to eliminate $T_A$ :

$W \times 1.5 + 20 \times 3 = T_C \times 1.8$

Solve for T_C:

1.8T_C = 1.5W + 60 \Rightarrow T_C = \frac{5}{6}W + \frac{100}{3} \text{ N}

Find the value of W:

Given $T_C = 8T_A$ and using the equilibrium condition $T_A + T_C = W + 20$ :
Substitute $T_C = 8T_A$ into the equation and solve for $W$ .

infoNote

Given:

$T_C$ is the tension at $C$ .
$T_A$ is the tension at $A.$
W is the weight of the pole.
The pole is in equilibrium.

Solution (b):

Find $T_A$ in terms of $W$

Using the equilibrium condition for vertical forces:

T_A + T_C - W - 20 = 0

Substitute $T_C = \frac{5}{6}W + \frac{100}{3}$ into the equation:

T_A + \left(\frac{5}{6}W + \frac{100}{3}\right) - W - 20 = 0

Solving for $T_A$ :

T_A = \frac{1}{6}W - \frac{40}{3}

Part (c):

infoNote

Given $T_C = 8T_A$ , find W

Substitute $T_C = 8T_A$ into the equation for $T_C$ :

\frac{5}{6}W + \frac{100}{3} = 8\left(\frac{1}{6}W - \frac{40}{3}\right)

Expanding and solving for $W$ :

\frac{5}{6}W + \frac{100}{3} = \frac{4}{3}W - \frac{320}{3}

Multiply the entire equation by $3$ to clear the fractions:

5W + 200 = 8W - 640

Simplifying:

840 = 3W \Rightarrow W = \frac{840}{3} = 280 \text{ N}

Result: The weight W of the pole is 280 N.

Tips:

infoNote

Identify the pivot point: Determine the point about which moments are taken (the pivot). Moments are calculated as $\text{Moment} = \text{Force} \times \text{Perpendicular Distance}$ , with clockwise moments usually taken as positive and anticlockwise as negative (or vice versa, as per convention).
Resolve all forces: Ensure all forces, including weights, reaction forces, and applied loads, are accounted for. If forces are acting at angles, resolve them into perpendicular components before calculating moments.
Apply the principle of moments: For equilibrium, the sum of clockwise moments equals the sum of anticlockwise moments about the pivot point. Use this to set up equations and solve for unknown forces or distances.

Moments Diagrams Simplified Revision Notes for A-Level OCR Maths Mechanics

4.1.1 Moments Diagrams

Moments

Problem 1: Jack and Jill on a Seesaw

Solution:

Problem 2: Q5, (Jan 2010, Q4) Tension in the Rope

Solution (a):

Given:

Solution (b):

Part (c):

Tips:

500K+ Students Use These Powerful Tools to Master Moments Diagrams For their A-Level Exams.

Other Revision Notes related to Moments Diagrams you should explore