Photo AI
Last Updated Sep 26, 2025
Proof by Exhaustion Simplified Revision Notes for A-Level OCR Maths Pure
Revision notes with simplified explanations to understand Proof by Exhaustion quickly and effectively.
457+ students studying
1.1.3 Proof by Exhaustion
In this type of proof, you consider every possible case to validate the proof.
Steps to Perform Proof by Exhaustion:
- Identify the statement to be proven and the possible cases that need to be considered.
- Break down the problem into a finite number of distinct cases. Make sure that all cases cover every possible scenario.
- Prove the statement for each case individually, showing that it holds true in each situation.
- Conclude that the statement is true for all cases, thereby proving the original statement.
Example: Prove that the sum of two odd numbers is always even for all cases involving single-digit odd numbers.
Step 1: Identify possible cases
The single-digit odd numbers are: 1, 3, 5, 7, 9
Step 2: List all pairings of odd numbers:
Step 3: Calculate each sum
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
- (even)
Step 4: Conclusion
Since all possible cases yield even results, we conclude that the sum of two odd numbers is always even.
This is an example of proof by exhaustion, as we've checked every possible case.
Example: Prove by exhaustion that 47 is prime.
- The idea: Check every possible factor of to see if an integer is obtained.
- : not a factor
- : not a factor
- : not a factor
- : not a factor
- : not a factor Note: Only need to go up to the last integer less than \sqrt{47}$$\ (= 6)
Conclusion
- Since all integers are not factors of ,
- Therefore, 47 is prime.
Alternative Method Using the Calculator
Steps:
- Go to table mode:
- Input the number we are checking as prime, denoted by a variable x:
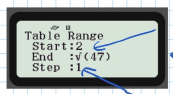
- Set start, end, and increment values:
- Start:
- End: Integer closest to but less than
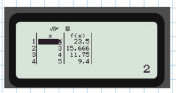
- Read off answers:
500K+ Students Use These Powerful Tools to Master Proof by Exhaustion For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Proof by Exhaustion
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards5 quizzes
Quizzes on Proof by Exhaustion
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes29 questions
Exam questions on Proof by Exhaustion
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Proof by Exhaustion
Create custom exams across topics for better practice!
Try Maths Pure exam builder12 papers
Past Papers on Proof by Exhaustion
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Proof by Exhaustion you should explore
Discover More Revision Notes Related to Proof by Exhaustion to Deepen Your Understanding and Improve Your Mastery
