Photo AI
Last Updated Sep 26, 2025
Completing the Square Simplified Revision Notes for A-Level OCR Maths Pure
Revision notes with simplified explanations to understand Completing the Square quickly and effectively.
242+ students studying
2.2.3 Completing the Square
- A complete square is a squared bracket (e.g., ).
- In a complete square, the coefficient of is often .
Example: Expand the following complete square
- Multiply and then square it.
Example: Write the following using a complete square
- gives us
- This move has an extra that we do not want; we must subtract to make it equal to the line above.
Example: Write in the form
Example: Complete the square for
- Complete the square for the underlined part:
Example: Write in the form :
- Much easier to work in fractions.
Further Completing the Square
- We only know how to complete the square for expressions of the form .
- This poses problems when completing the square for something of the form where .
Example: Complete the square for
Take out factor of so that we have something that says .
Ensure this is equal to the line above.
Multiply out square brackets.
You can multiply out to check it is equal to original answer.
Example: Write in the form :
$-x^2 + 10x - 5 \
= -[x^2 - 10x] - 5
\ = -[(x - 5)^2 - 25] - 5 \
= -(x - 5)^2 + 25 - 5
\ = -(x - 5)^2 + 20$
Example (Q4. Jun 2008, Q10) [Modified]: Express in the form :
Application of Completing the Square
- Take, for example, .
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|---|---|---|---|
| 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | |
| 12 | 7 | 4 | 3 | 4 | 7 | 12 | 19 | 28 |
-
The are symmetrical about .
-
The reason for this symmetry is that when , the squared bracket is equal to 0. Increasing or decreasing what is in the bracket by results in a symmetrical pattern.
-
Leads to the same number but with a different sign.
-
By the time we square it, the answers are both the same number and both positive.
-
Using this information to sketch the curve, we get:
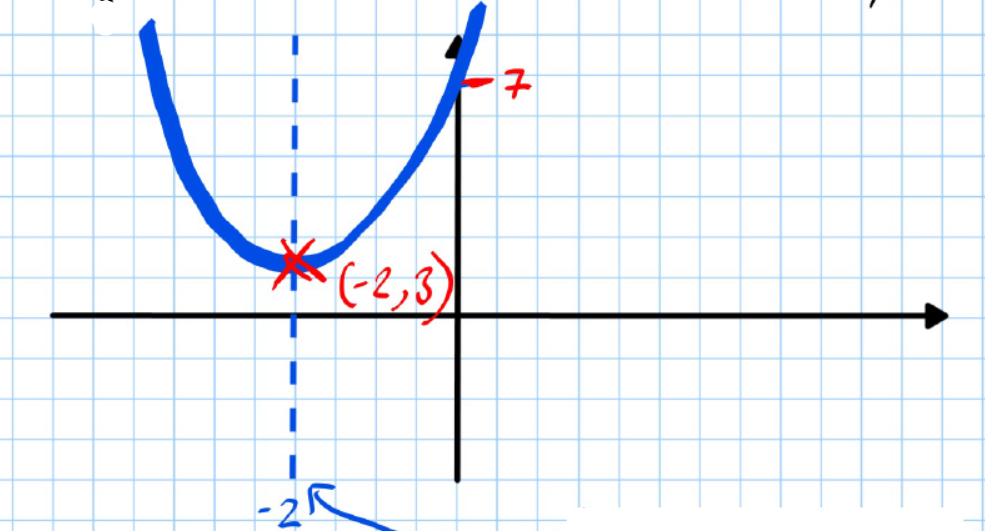
-
Symmetrical about .
-
When , .
-
When , .
Example: Find the coordinates of the vertex of :
- Note: A vertex of a quadratic is its turning (max/min) point.
is when
makes
Example: Find the equation of the tangent to the following curve at its vertex and the corresponding line of symmetry. Use this to sketch the curve:
- Completing the Square:
- Vertex:
Graph and Line of Symmetry:
- , not .
- Kinks and looks like the graph is about to go back down.
- Key points are not labelled.
- Line of symmetry:
- Tangent:
Q1 (Jun 2005, Q2): 2. Express :
- Equation of the line of symmetry of the curve :
- Key Points:
- is the line of symmetry.
- The vertex is at .
- Illustration:
- Left: Tangent
- Right: Vertex
500K+ Students Use These Powerful Tools to Master Completing the Square For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
60 flashcards
Flashcards on Completing the Square
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards6 quizzes
Quizzes on Completing the Square
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes29 questions
Exam questions on Completing the Square
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Completing the Square
Create custom exams across topics for better practice!
Try Maths Pure exam builder12 papers
Past Papers on Completing the Square
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Completing the Square you should explore
Discover More Revision Notes Related to Completing the Square to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Quadratics
Further Solving Quadratic Equations (Hidden Quadratics)
399+ studying
183KViews