Photo AI
Last Updated Sep 26, 2025
Reciprocal Graphs - Sketching Simplified Revision Notes for A-Level OCR Maths Pure
Revision notes with simplified explanations to understand Reciprocal Graphs - Sketching quickly and effectively.
256+ students studying
2.7.2 Reciprocal Graphs - Sketching
Sketching Reciprocal Graphs
Reciprocal graphs are graphs of functions that have the form:
where is a constant, or more generally:
These graphs are important because they illustrate inverse relationships and can exhibit asymptotic behaviour, where the graph approaches a line but never touches it.
Steps to Sketch Reciprocal Graphs
Identify the Basic Form:
-
The most basic reciprocal graph is , which can be modified by changing the value of or by adding transformations. Determine Asymptotes:
-
Vertical Asymptote: The graph has a vertical asymptote where the denominator is zero. For , this is at . For set to find the vertical asymptote.
-
Horizontal Asymptote: The graph has a horizontal asymptote as approaches infinity or negative infinity. For , this is . Similarly, for , the horizontal asymptote is . Identify Key Points:
-
Consider specific values of to determine key points on the graph. For example:
-
-
-
These points help establish the general shape of the graph. Consider Symmetry:
-
The graph of is symmetric about the origin (rotational symmetry of degrees).
-
If , the graph lies in the first and third quadrants. If , it lies in the second and fourth quadrants. Plot the Graph:
-
Plot the vertical and horizontal asymptotes.
-
Plot key points, such as where and others as necessary.
-
Sketch the graph, ensuring it approaches the asymptotes but never touches them.
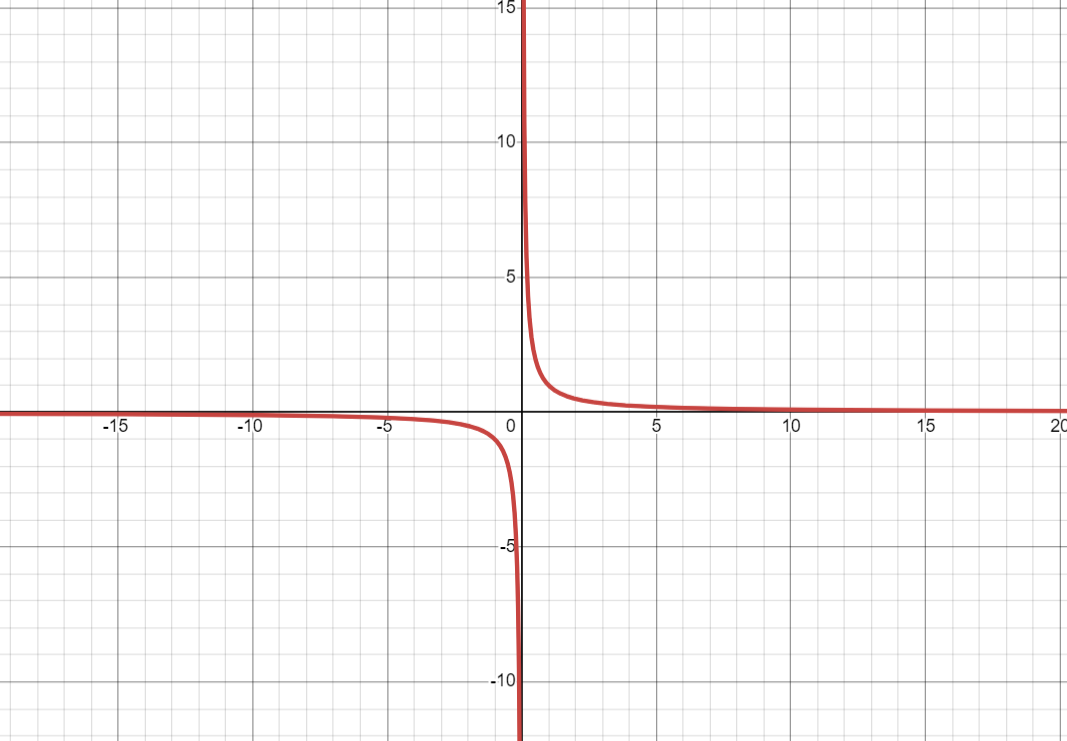
Example 1: Basic Reciprocal Graph
Graph
- Asymptotes:
- Vertical asymptote at .
- Horizontal asymptote at
- Key Points:
- At .
- At
- Symmetry:
- The graph is symmetric about the origin.
- Sketch:
- The graph passes through and , and it approaches the asymptotes.
Example 2: Transformed Reciprocal Graph
Graph :
- Asymptotes:
- Vertical asymptote where
- Horizontal asymptote at
- Key Points:
- At
- At
- Sketch:
- The graph passes through
- It approaches the vertical asymptote and the horizontal asymptote
Summary:
- Asymptotes: Identify where the graph will have vertical and horizontal asymptotes.
- Key Points: Calculate values for key points on the graph, such as where
- Symmetry: Consider the symmetry of the graph to guide your sketching.
- Plot and Sketch: Combine the asymptotes, key points, and symmetry to sketch the graph.
By following these steps, you can accurately sketch reciprocal graphs, which are crucial for understanding inverse relationships and behaviours in mathematics.
500K+ Students Use These Powerful Tools to Master Reciprocal Graphs - Sketching For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Reciprocal Graphs - Sketching
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards5 quizzes
Quizzes on Reciprocal Graphs - Sketching
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes29 questions
Exam questions on Reciprocal Graphs - Sketching
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Reciprocal Graphs - Sketching
Create custom exams across topics for better practice!
Try Maths Pure exam builder12 papers
Past Papers on Reciprocal Graphs - Sketching
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Reciprocal Graphs - Sketching you should explore
Discover More Revision Notes Related to Reciprocal Graphs - Sketching to Deepen Your Understanding and Improve Your Mastery
