2.8.3 Inverse Functions

Inverse of a Function

A function only has an inverse if it is one-to-one ($1$-to-$1$).

• Example: $f(x) = x^2, x \in \mathbb{R}$ has no inverse.
• Function is many-to-one, therefore no inverse exists.

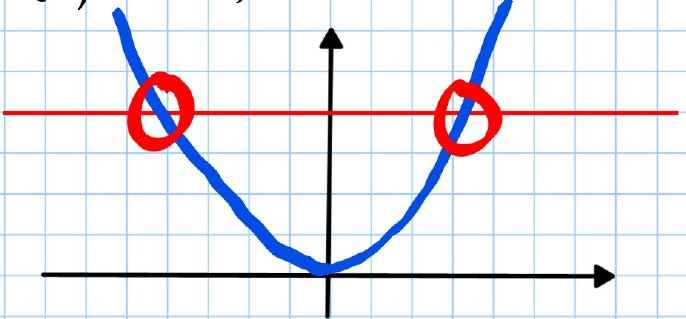
However, we can "artificially" restrict the domain of a function to make it one-to-one ($1$-to-$1$), thus forcing the existence of an inverse.

• Example: $f(x) = x^2, x \geq 0$
• One-to-one, therefore has an inverse.

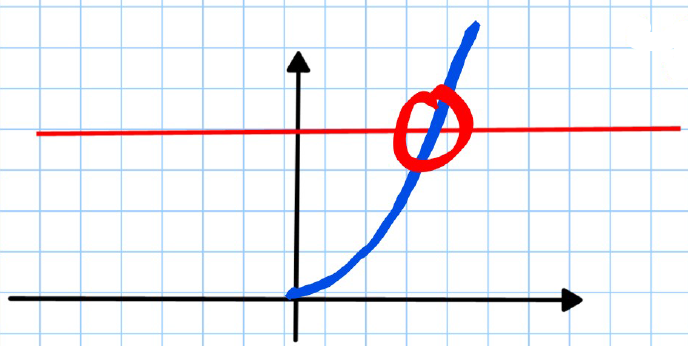
The inverse of a function is denoted $f^{-1}(x)$ for a function $f(x)$.

• For $f(x) = x^2, x \geq 0$: $f^{-1}(x) = \sqrt{x}$

---

Steps to Find the Inverse of a Function

---

---

Geometric Relationship Between a Function and its Inverse

To find the inverse of a function, we simply swap its $x$ and y values. This is the equivalent of reflecting the graph through the line $y = x$.

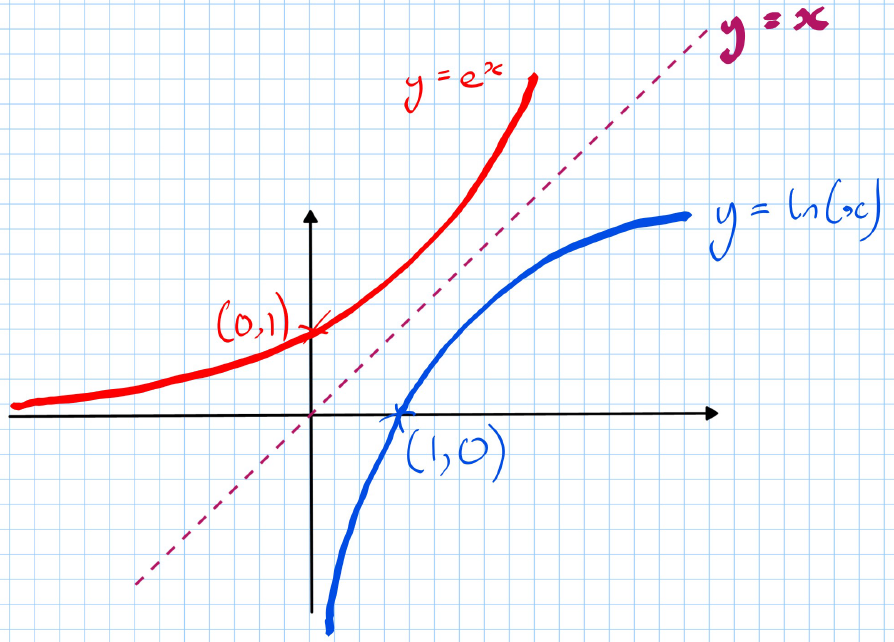
Graphical Representation:

• The graph shows the functions $y = e^x$ (red curve) and $y = \ln(x)$ (blue curve) with the line $y = x$ as a dotted diagonal line.
• Key points marked on the graph:
  • (0,1) on $y = e^x$
  • (1,0) on $y = \ln(x)$

---

---