Photo AI
Last Updated Sep 27, 2025
Radius & Tangent Simplified Revision Notes for A-Level OCR Maths Pure
Revision notes with simplified explanations to understand Radius & Tangent quickly and effectively.
470+ students studying
3.2.5 Radius & Tangent
Tangents and Normal to Circles
- Tangent: A tangent is a line that just touches a circle but does not cut it.
- Normal (or radius): A normal is at right angles to a tangent.
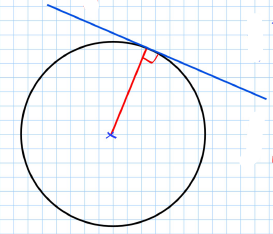
Radius:
- The radius of a circle is the distance from the centre of the circle to any point on its circumference.
- In a circle equation of the form , the radius is r, and the centre is at (h, k).
- If the equation of the circle is (a circle centred at the origin), then the radius is .
- Example: For , the radius is .
Key Properties of a Radius:
- All radii of a circle are equal in length.
- A radius is always perpendicular to the tangent at the point of contact.
Tangent to a Circle:
- A tangent to a circle is a straight line that touches the circle at exactly one point. This point is called the point of tangency.
- The tangent to a circle is perpendicular to the radius at the point of tangency.
- The equation of the tangent to a circle with equation at a point on the circle is given by:
This is derived from the fact that the tangent is perpendicular to the radius at the point of tangency.
Key Properties of Tangents:
- A tangent touches the circle at only one point.
- A tangent to a circle is always perpendicular to the radius at the point of tangency.
- From a point outside the circle, you can draw two tangents to the circle. These tangents are equal in length.
Example of Tangent Equation:
For a circle with equation :
- At point , the tangent would be:
This is a vertical line, tangent to the circle at .
- At point , the tangent would be:
This is a horizontal line, tangent to the circle at .
Relationship Between Radius and Tangent:
The most important relationship between the radius and the tangent is perpendicularity. At any point of tangency, the radius drawn to that point is perpendicular to the tangent.
These are the foundational notes on radius and tangent in the context of a circle.
Example: Find the equation of the tangent to the circle
at the point .
- Rewrite the circle equation:
- Completing the square for reveals the centre of the circle: .
- Find the centre:
- The centre of the circle is .
- Find the gradient of the normal:
- Gradient of the normal is 4.
- Find the gradient of the tangent:
- The gradient of the tangent is the negative reciprocal of the gradient of the normal.
- Equation of the tangent:
- Using the point-slope form of the line equation.
- Simplify the equation:
Final Equation
This is the equation of the tangent to the circle at the point .
Tangents and Circles: Finding
Problem:
The line with the equation is a tangent to the circle with the equation . Find the two possible values of .
Solution:
-
Substitute into the circle equation:
-
Expand and simplify:
-
Group the terms:
-
Identify coefficients for the quadratic equation in terms of :
- Since the line is a tangent, the quadratic equation has exactly one solution:
- This implies the discriminant must be zero.
- Substitute the values of , and into the discriminant formula:
- Solve the quadratic equation:
- Factorise or use the quadratic formula:
Final Values of
500K+ Students Use These Powerful Tools to Master Radius & Tangent For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
60 flashcards
Flashcards on Radius & Tangent
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards6 quizzes
Quizzes on Radius & Tangent
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes29 questions
Exam questions on Radius & Tangent
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Radius & Tangent
Create custom exams across topics for better practice!
Try Maths Pure exam builder12 papers
Past Papers on Radius & Tangent
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Radius & Tangent you should explore
Discover More Revision Notes Related to Radius & Tangent to Deepen Your Understanding and Improve Your Mastery
