Photo AI
Last Updated Sep 27, 2025
Reciprocal Trig Functions - Graphs Simplified Revision Notes for A-Level OCR Maths Pure
Revision notes with simplified explanations to understand Reciprocal Trig Functions - Graphs quickly and effectively.
286+ students studying
5.5.2 Reciprocal Trig Functions - Graphs
The graphs of the reciprocal trigonometric functions—cosecant , secant , and cotangent —are derived from the basic trigonometric functions sine, cosine, and tangent, respectively. Understanding these graphs is important for visualizing the behaviour of these functions and recognizing their key features such as asymptotes and periodicity.
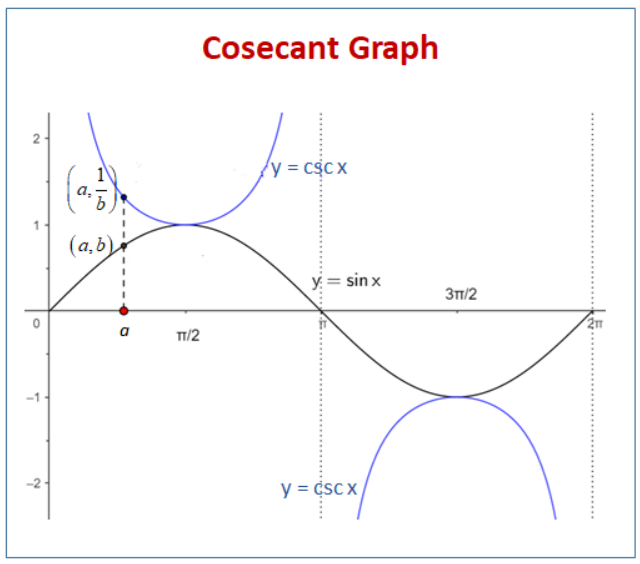
1. Graph of Cosecant ():
- Definition:
- The cosecant function is undefined where , which occurs at
- Asymptotes:
- Vertical asymptotes occur where so the graph has vertical asymptotes at
- Shape:
- Between these asymptotes, the graph has branches that mirror the sine wave but are flipped and stretched.
- The graph approaches infinity as approaches the asymptotes from either side.
- At the peaks of the sine function (where (), the cosecant function will intersect at or (), respectively.
- Periodicity:
- The period of the function is the same as , which is or radians.
Graph Characteristics Summary:
- Vertical Asymptotes: where is an integer.
- Range:
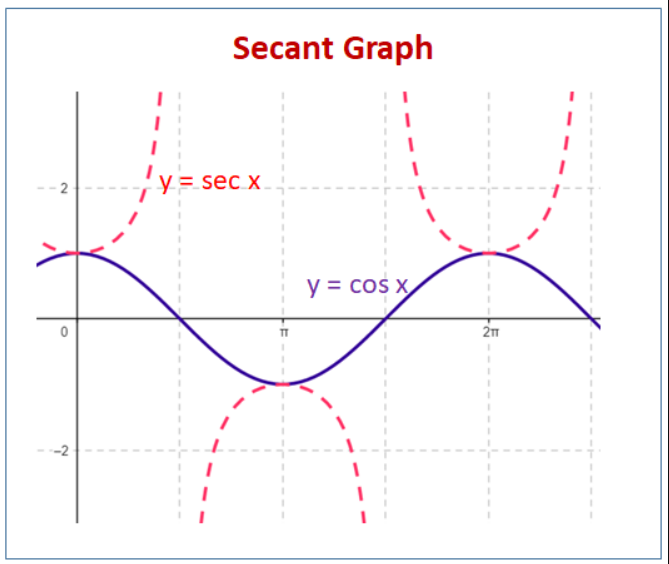
2. Graph of Secant ():
- Definition:
- The secant function is undefined where , which occurs at
- Asymptotes:
- Vertical asymptotes occur where , so the graph has vertical asymptotes at
- Shape:
- The graph of consists of upward and downward branches that mirror the cosine wave, flipped and stretched.
- At the points where (the maximum and minimum values of cosine), the secant function intersects at and , respectively.
- As approaches the asymptotes, the secant function approaches infinity.
- Periodicity:
- The period of the function is the same as , which is radians.
Graph Characteristics Summary:
- Vertical Asymptotes: , where is an integer.
- Range:
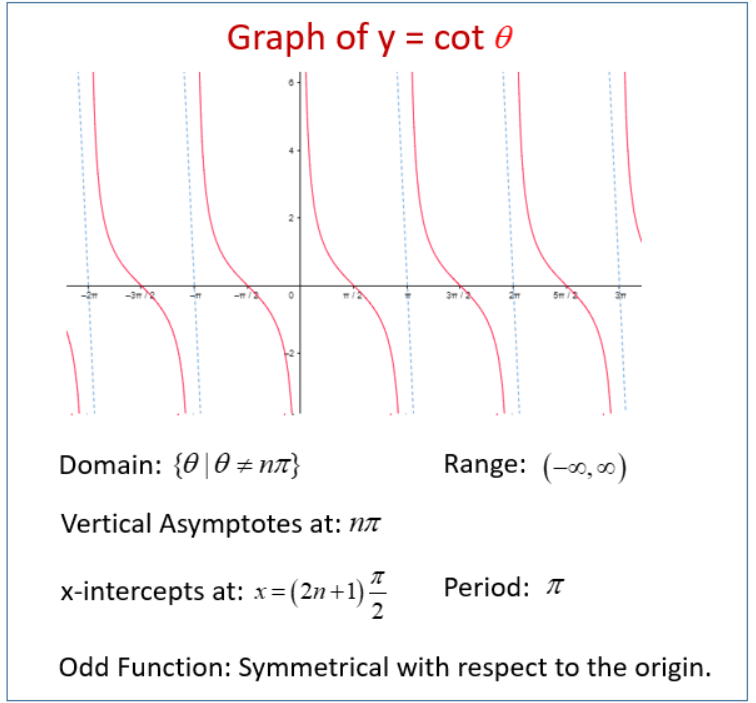
3. Graph of Cotangent ():
- Definition:
- The cotangent function is undefined where , which occurs at
- Asymptotes:
- Vertical asymptotes occur where , so the graph has vertical asymptotes at
- Shape:
- The graph of is a decreasing curve between each pair of vertical asymptotes, reflecting the fact that the cotangent function decreases as increases within each interval.
- Unlike the tangent function, which increases from negative to positive infinity, the cotangent function decreases from positive to negative infinity as increases.
- Periodicity:
- The period of the function is or radians, which is half the period of the sine and cosine functions.
Graph Characteristics Summary:
- Vertical Asymptotes: , where is an integer.
- Range:
Summary of Reciprocal Trig Function Graphs:
- Cosecant (): Graph has vertical asymptotes where. The graph consists of upward and downward branches that approach infinity near the asymptotes.
- Secant (): Graph has vertical asymptotes where . The graph consists of upward and downward branches similar to cosecant but aligned with the cosine function.
- Cotangent (): Graph has vertical asymptotes where . The graph is a series of decreasing curves between each pair of asymptotes, with a period of radians.
500K+ Students Use These Powerful Tools to Master Reciprocal Trig Functions - Graphs For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Reciprocal Trig Functions - Graphs
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards5 quizzes
Quizzes on Reciprocal Trig Functions - Graphs
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes29 questions
Exam questions on Reciprocal Trig Functions - Graphs
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Reciprocal Trig Functions - Graphs
Create custom exams across topics for better practice!
Try Maths Pure exam builder12 papers
Past Papers on Reciprocal Trig Functions - Graphs
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Reciprocal Trig Functions - Graphs you should explore
Discover More Revision Notes Related to Reciprocal Trig Functions - Graphs to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Reciprocal & Inverse Trigonometric Functions
Reciprocal Trig Functions - Definitions
431+ studying
184KViews96%
114 rated
Reciprocal & Inverse Trigonometric Functions
Trigonometry - Further Identities
350+ studying
193KViews96%
114 rated
Reciprocal & Inverse Trigonometric Functions
Inverse Trig Functions
231+ studying
194KViews