Photo AI
Last Updated Sep 27, 2025
Second Order Derivatives Simplified Revision Notes for A-Level OCR Maths Pure
Revision notes with simplified explanations to understand Second Order Derivatives quickly and effectively.
233+ students studying
7.2.3 Second Order Derivatives
Second order derivatives are the derivatives of the first derivative of a function. They provide insight into the curvature of the function and are crucial for understanding the concavity and inflection points of the function, as well as for determining acceleration in physical contexts.
1. Definition of Second Order Derivative:
If is a function, its first derivative represents the rate of change of with respect to The second derivative is the derivative of representing the rate of change of the first derivative.
- Mathematically: Here, denotes the second derivative of with respect to
2. Interpretation of the Second Derivative:
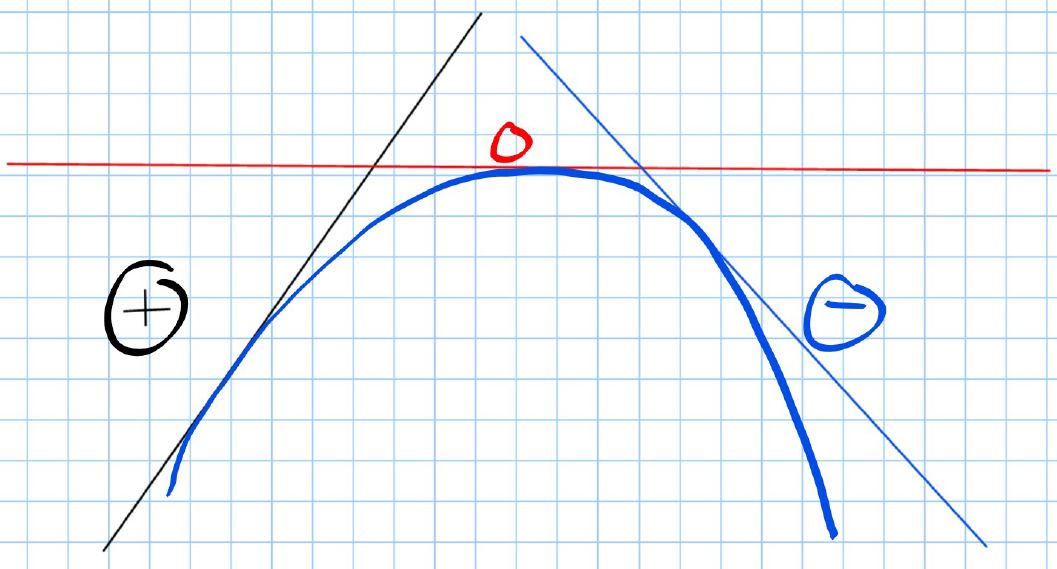
- Concavity: The second derivative tells us about the concavity of the graph of a function:
- Concave Up: If for all in an interval, the graph of is concave up (shaped like a ) on that interval.
- Concave Down: If for all in an interval, the graph of is concave down (shaped like an inverted U) on that interval.
- Inflection Points: An inflection point is a point on the graph of where the concavity changes (i.e., the graph changes from concave up to concave down, or vice versa). These points occur where the second derivative changes sign (from positive to negative or from negative to positive).
3. Steps to Calculate the Second Derivative:
- Find the First Derivative: Start by calculating the first derivative of the function
- Differentiate Again: Take the derivative of to obtain the second derivative .
4. Example Problems Involving Second Derivatives:
Example 1: Find the second derivative of .
- Step 1: Find the first derivative:
- Step 2: Find the second derivative:
- Interpretation:
- The second derivative tells us about the concavity of the function . The sign of will determine where the function is concave up or concave down.
- when , indicating the function is concave up for
- when , indicating the function is concave down for .
- There is an inflection point at , where the concavity changes.
Example 2: Find the inflection point(s) of
- Step 1: Find the first derivative:
- Step 2: Find the second derivative:
- Step 3: Set to find potential inflection points:
- Step 4: Check the sign of :
- The second derivative is non-negative for all, meaning it is at and positive elsewhere. There is no change in concavity at is not an inflection point.
- Conclusion:
- Since does not change sign at does not have an inflection point.
5. Applications of Second Derivatives:
- Optimization: In optimization problems, the second derivative test helps determine whether a critical point is a local maximum, local minimum, or saddle point.
- If at a critical point is a local minimum.
- If at a critical point is a local maximum.
- If at a critical point the test is inconclusive, and further analysis is needed.
- Physics: In kinematics, the second derivative of the position function with respect to time gives the acceleration of an object.
- Economics: The second derivative is used to analyse the curvature of cost functions, utility functions, and other economic models.
Summary:
- Second order derivatives provide valuable information about the curvature of a function, indicating where the function is concave up or concave down.
- Inflection points occur where the second derivative changes sign, marking a change in the concavity of the function.
- The second derivative is widely used in optimization, physics, and economics to analyse and predict the behaviour of functions and systems.
The Second Differential
The second differential/derivative tells us the rate of change of gradient and is denoted by:
or
If , this means the gradient is increasing.
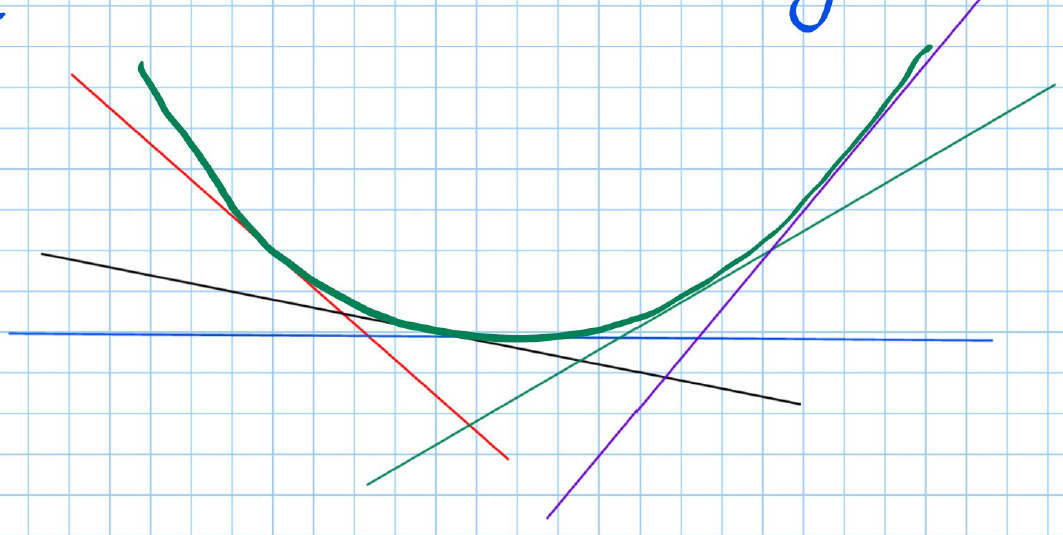
- Very negative less negative 0 a little positive more positive
Similarly, if , the gradient is decreasing.
500K+ Students Use These Powerful Tools to Master Second Order Derivatives For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
70 flashcards
Flashcards on Second Order Derivatives
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards7 quizzes
Quizzes on Second Order Derivatives
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes29 questions
Exam questions on Second Order Derivatives
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Second Order Derivatives
Create custom exams across topics for better practice!
Try Maths Pure exam builder12 papers
Past Papers on Second Order Derivatives
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Second Order Derivatives you should explore
Discover More Revision Notes Related to Second Order Derivatives to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Applications of Differentiation
Gradients, Tangents & Normal
368+ studying
180KViews96%
114 rated
Applications of Differentiation
Increasing & Decreasing Functions
500+ studying
183KViews96%
114 rated
Applications of Differentiation
Stationary Points & Turning Points
244+ studying
192KViews96%
114 rated
Applications of Differentiation
Sketching Gradient Functions
448+ studying
200KViews