Binary Shifts

Binary shifts are operations that move the bits of a binary number either to the left or right. This process can change the value of the binary number, either making it larger or smaller, depending on the direction of the shift.

Types of Binary Shifts

Left Shift

Moves the binary number to a set number of places to the left.

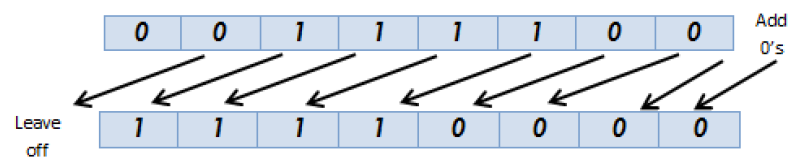
Effect: Increases the value of the number (multiplied by powers of 2).
Example: A left shift of 1 is equivalent to multiplying the number by 2. A left shift of 2 multiplies it by 4.
Important Note: Any gaps created on the right are filled with 0s.

Example

infoNote

Question: Left shift 00111100 (60 in denary) by 2 places.

Step 1: Start with the original binary number

The original binary number is 00111100.
In denary (decimal), this is 60.

Step 2: Perform the left shift

A left shift moves each bit 2 places to the left.
When shifting left, the leftmost bits move, and the empty spaces on the right are filled with 0.
Original binary number: 00111100
After 2 left shifts: 11110000

Step 3: Convert the result to denary

The new binary number is 11110000.
To convert this back to denary:
The binary number 11110000 represents the following values:

1×2^7=128

1×2^6 = 64

1×2^5 = 32

1×2^4 = 16

0×2^3 = 0

0×2^2 = 0

0×2^1 = 0

0×2^0 = 0

Total: 128 + 64 + 32 + 16 = 240

Step 4: Explanation of the effect

The binary number 00111100 (60 in denary) was shifted 2 places to the left, which is equivalent to multiplying the original number by (2^2 = 4).
After the shift, the result is 11110000 (240 in denary).
Therefore, the left shift by 2 is like multiplying 60 by 4 to get 240.

Key Takeaway

Left shifting by 2 multiplies the number by 4.
00111100 (60) becomes 11110000 (240) after the shift.

Right Shift

Moves the binary number to a set number of places to the right.

Effect: Decreases the value of the number (divided by powers of 2).
Example: A right shift of 1 is equivalent to dividing the number by 2. A right shift of 2 divides it by 4.
Important Note: Any bits that are shifted out on the right are discarded. Gaps on the left are filled with 0s, but this can result in loss of accuracy (especially when dividing).

Worked Example

infoNote

Question: Right shift 00111100 (60 in denary) by 1 place.

Step 1: Start with the original binary number

The original binary number is 00111100.
In denary (decimal), this is 60.

Step 2: Perform the right shift

A right shift moves each bit 1 place to the right.
When shifting right, the rightmost bit "falls off" and is discarded.
The empty space on the left is filled with 0.
Original binary number: 00111100
After 1 right shift: 00011110

Step 3: Convert the result to denary

The new binary number is 00011110.
To convert this back to denary:
The binary number 00011110 represents the following values:

0×2^7=0

0×2^6 = 0

0×2^5 = 0

1×2^4 = 16

1×2^3 = 8

1×2^2 = 4

1×2^1 = 2

0×2^0 = 0

Total: 16 + 8 + 4 + 2 = 30

Step 4: Explanation of the effect

The binary number 00111100 (60 in denary) was shifted 1 place to the right, which is equivalent to dividing the original number by 2.
After the shift, the result is 00011110 (30 in denary).
Therefore, the right shift by 1 is like dividing 60 by 2 to get 30.

Key Takeaway

Right shifting by 1 divides the number by 2.
00111100 (60) becomes 00011110 (30) after the shift.

Understanding Binary Shifts

Left Shift Summary

Shifts bits to the left.
Increases the value of the binary number (multiplication by powers of 2).
Gaps on the right are filled with 0s.
Effect: The number grows larger.

Right Shift Summary

Shifts bits to the right.
Decreases the value of the binary number (division by powers of 2).
Gaps on the left are filled with 0s, and bits that fall off the right are lost.
Effect: The number becomes smaller.

Examples of Binary Shifts

Shift Type	Description	Example
Left Shift	Shifting a binary number left multiplies it by 2 for each place shifted.	00111100 (60 in denary) left-shifted by 2 becomes 11110000 (240 in denary).
Right Shift	Shifting a binary number right divides it by 2 for each place shifted, losing bits on the right.	00111100 (60 in denary) right-shifted by 1 becomes 00011110 (30 in denary).

infoNote

Key Points

Left shifts increase the value of the number by powers of 2.
Right shifts decrease the value of the number by powers of 2.
Shifting can result in lost information when bits "fall off" in a right shift.

Binary Shifts Simplified Revision Notes for GCSE OCR Computer Science

Binary Shifts

Types of Binary Shifts

Left Shift

Example

Question: Left shift 00111100 (60 in denary) by 2 places.

Right Shift

Worked Example

Question: Right shift 00111100 (60 in denary) by 1 place.

Understanding Binary Shifts

Left Shift Summary

Right Shift Summary

Examples of Binary Shifts

Key Points

500K+ Students Use These Powerful Tools to Master Binary Shifts For their GCSE Exams.

Other Revision Notes related to Binary Shifts you should explore