Fractions

Things You Should Know About Fractions:

Numerator: The top part of a fraction, representing how many parts of the whole you have.
Denominator: The bottom part of a fraction, representing how many equal parts the whole is divided into.

infoNote

Example: In the fraction $\frac{3}{4}$ :

$3$ is the numerator.
$4$ is the denominator.

Fraction of a Quantity

To find a fraction of a quantity, follow these simple steps:
1. Divide by the Denominator: This gives the value of one part.
2. Multiply by the Numerator: This gives the value of the required parts. Worked Examples

infoNote

Example 1: Finding a Fraction of a Quantity

Problem: What is $\frac{3}{4}$ of $24$ ?
Steps:

Divide by the denominator:

\frac{24}{6} =6

Multiply by the numerator:

6×3=18

Result: $\frac{3}{4}$ of $24$ is 18.

infoNote

Example 2: Fraction of a Quantity with Units

Problem: Find $\frac{5}{7}$ of $2436$ grams.
Steps:

Divide by the denominator:

\frac{2436}{7}=348

Multiply by the numerator:

348×5=1740

Result: $\frac{5}{7}$ of $2436$ grams is 1740 grams

Equivalent Fractions

Equivalent fractions are fractions that represent the same value, even though they may look different. Understanding how to identify and work with equivalent fractions is essential for simplifying answers and performing operations like addition and subtraction of fractions.

What Are Equivalent Fractions?

Equivalent fractions are fractions that have the same value. For instance, $\frac{1}{2}$ is equivalent to $\frac{2}{4}$ because both represent the same proportion of the whole.

🔑 Key Rule:

To create an equivalent fraction, whatever you multiply or divide the top (numerator) by, do the exact same to the bottom (denominator)!

Worked Examples

infoNote

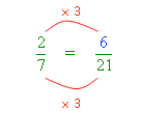
Example 1: Creating an Equivalent Fraction

Problem: Find an equivalent fraction for $\frac{2}{7}$ with a denominator of $21$ .
Steps:

Ask yourself: "What has been done to the $7$ to make it $21$ ?"

Answer: $7×3=21.$

Do the same to the numerator:

Multiply $2$ by $3$ :

2×3=6

Result: The equivalent fraction is $\frac{6}{21}$ .

Visual Representation:

infoNote

Example 2: Identifying an Equivalent Fraction

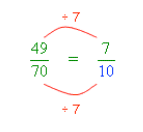
Problem: Identify what $\frac{49}{70}$ is equivalent to when the numerator is reduced to $7$ .
Steps:

Ask yourself: "What has been done to the $49$ to make it $7$ ?"

Answer: $49÷7=7$ .

Do the same to the denominator:

Divide $70$ by $7$ :

70÷7=10

Result: The equivalent fraction is $\frac{7}{10}$ .

Visual Representation:

infoNote

Example 3: Simplifying a Fraction

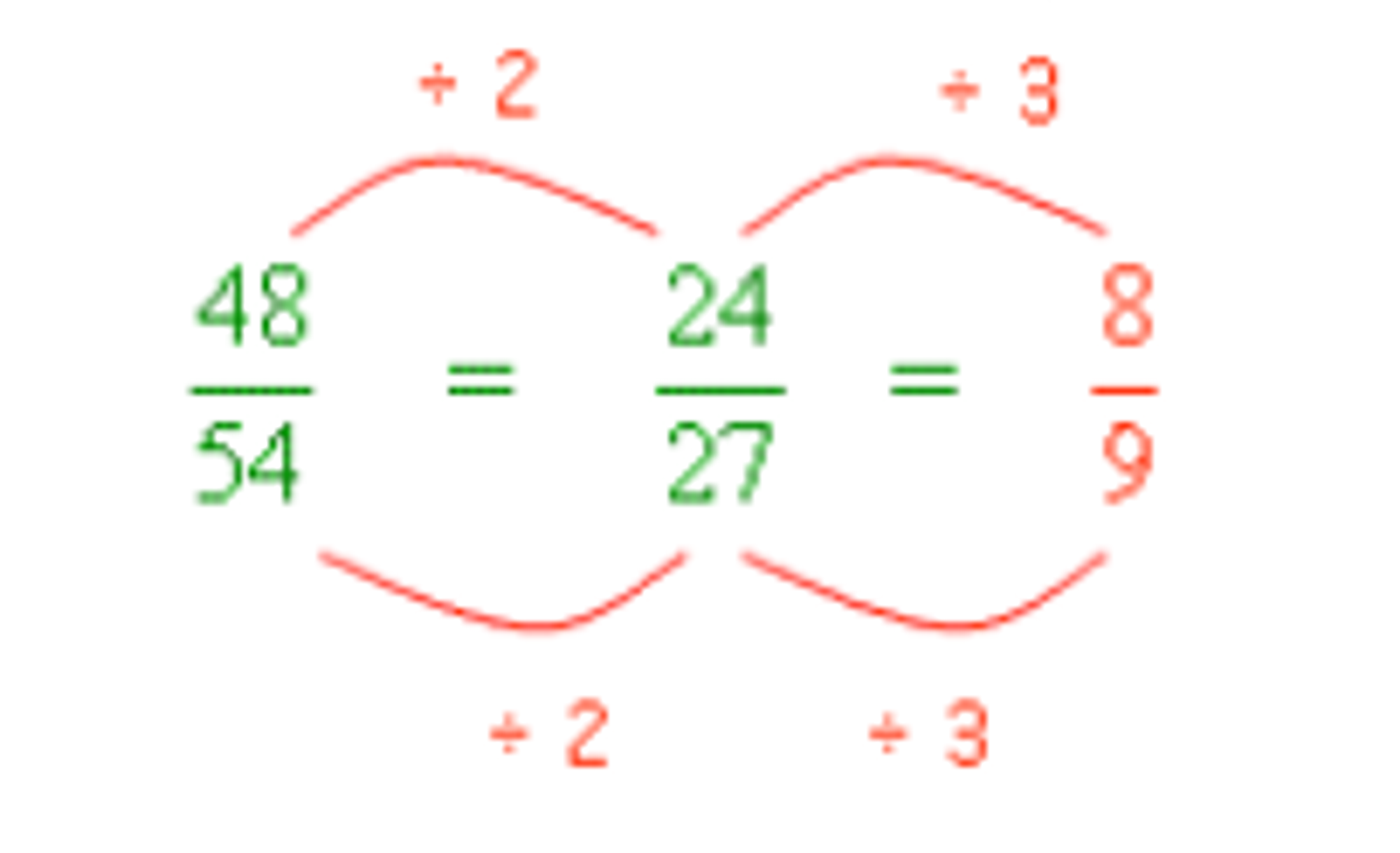
Problem: Simplify the fraction $\frac{48}{54}$ .
Steps:

Find a common factor that divides both the numerator and the denominator. Start by dividing by $2$ :

\frac{48 \div 2}{54 \div 2} = \frac{24}{27}

Now, divide both by $3$ :

\frac{24 \div 3}{27 \div 3} = \frac{8}{9}

Result: The simplified fraction is $\frac{8}{9}$ .

Visual Representation:

Proper and Improper Fractions

Definitions:

Proper Fraction: A fraction where the numerator (top number) is smaller than the denominator (bottom number). This type of fraction represents a part of a whole that is less than one.
Example: $\frac{3}{4}, \frac{2}{5}$ $\frac{3}{4}, \frac{2}{5}$
- Improper Fraction: A fraction where the numerator is equal to or greater than the denominator. This type of fraction represents a value that is equal to or greater than one whole.
Example: $\frac{9}{7}, \frac{22}{5}$ $\frac{9}{7}, \frac{22}{5}$
- Mixed Number: A combination of a whole number and a proper fraction, used to express an improper fraction.
Example: $3 \frac{2}{7}$

Converting Improper Fractions to Mixed Numbers:

infoNote

Example 1: Convert $\frac{22}{5}$ to a Mixed Number

Step 1: Divide the numerator by the denominator: $22÷5=4$ with a remainder of $2$
The quotient ( $4$ ) represents the whole number.
The remainder ( $2$ ) becomes the numerator of the proper fraction.
Step 2: Write the remainder over the original denominator:

\text{So,} \ \frac{22}{5} = 4 \frac{2}{5}

Result: The improper fraction $\frac{22}{5}$ is equivalent to the mixed number $4 \frac{2}{5}$ .

Converting Mixed Numbers to Improper Fractions:

infoNote

Example 2: Convert $3 \frac{5}{8}$ to an Improper Fraction

Step 1: Multiply the whole number by the denominator:

3×8=24

Step 2: Add the result to the numerator:

24+5=29

The sum becomes the numerator of the improper fraction.
Step 3: Write the result over the original denominator:

\text{So, } 3 \frac{5}{8} = \frac{29}{8}

Result: The mixed number $3 \frac{5}{8}$ is equivalent to the improper fraction $\frac{29}{8}$ .

Adding, Subtracting, Multiplying, and Dividing Fractions

(a) Adding and Subtracting Fractions

Important Reminder:

Never add or subtract fractions by adding or subtracting the numerators and denominators directly. This approach is incorrect and will not give you the correct answer.

Correct Steps for Adding and Subtracting Fractions:

Convert Mixed Numbers: If your fractions are in mixed number form, first convert them into improper fractions (top-heavy).
Common Denominator: Ensure both fractions have the same denominator. To do this:

Choose the lowest common multiple (LCM) of both denominators.
Convert both fractions so that they share this common denominator.

Add or Subtract the Numerators: Once the denominators are the same, add or subtract the numerators, keeping the denominator the same.
Simplify: If possible, simplify the resulting fraction to its lowest terms.

infoNote

Example 1: Adding Fractions

infoNote

Example 2: Subtracting Fractions

Problem: $\frac{4}{15} - \frac{1}{5}$
Steps:

Find a common denominator:

The LCM of $15$ and $5$ is $15$ .
Convert $\frac{1}{5}$ to $\frac{3}{15}$ .

Subtract the numerators:

\frac{4}{15} + \frac{3}{15}= \frac{1}{15}

Result: The difference is $\frac{1}{15}$ .

(b) Multiplying and Dividing Fractions

Multiplying Fractions:

Convert Mixed Numbers: Convert any mixed numbers to improper fractions.
Multiply the Numerators Together: Multiply the top numbers (numerators) together.
Multiply the Denominators Together: Multiply the bottom numbers (denominators) together.
Simplify: Simplify the resulting fraction to its lowest terms.

infoNote

Example 1: Multiplying Fractions

Problem: $\frac{2}{3} × \frac{4}{7}$
Steps:

Multiply the numerators:

2×4=8

Multiply the denominators:

3×7=21

Result: The product is $\frac{8}{21}$ .

(c) Dividing Fractions:

Convert Mixed Numbers: Convert any mixed numbers to improper fractions.
Flip the Second Fraction: Invert (flip) the second fraction.
Multiply: Multiply the first fraction by the flipped second fraction.
Simplify: Simplify the resulting fraction.

infoNote

Example 2: Dividing Fractions

Problem: $\frac{3}{7} ÷ \frac{2}{5}$
Steps:

Flip the second fraction:

\frac{2}{5} becomes \frac{5}{2}

Change to multiplication:

\frac{3}{7} × \frac{5}{2}

Multiply the numerators:

3×5=15

Multiply the denominators:

7×2=14

Result: The quotient is $\frac{15}{14}$ .

Fractions, Decimals, and Percentages

Fractions, decimals, and percentages are closely related, and being able to convert between them is an essential skill

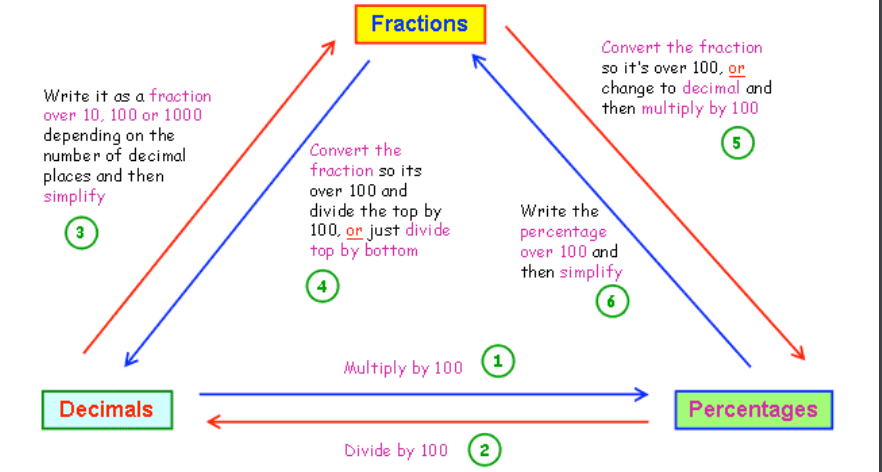
Converting Between Fractions, Decimals, and Percentages:

1. Converting a Decimal to a Percentage

infoNote

Example: Convert $0.364$ to a percentage.
Steps:

Multiply the decimal by $100$ :

0.364×100=36.4%

Result: $0.364$ as a percentage is 36.4%.

2. Converting a Percentage to a Decimal

infoNote

Example: Convert $8.3%$ to a decimal.
Steps:

Divide the percentage by $100$ :

8.3÷100=0.083

Result: $8.3%$ as a decimal is 0.083.

3. Converting a Decimal to a Fraction

infoNote

Example: Convert $0.16$ to a fraction.
Steps:

Write the decimal as a fraction with the denominator as $100$ (since there are two decimal places):

0.16 = \frac{16}{100}

Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is $4$ in this case:

\frac{16}{100} = \frac{4}{25}

Result: $0.16$ as a fraction is $\frac{4}{25}$ .

4. Converting a Fraction to a Decimal

infoNote

Example: Convert $\frac{13}{20}$ to a decimal.
Steps:

Adjust the fraction so that the denominator is $100$ (multiply both the numerator and the denominator by $5$ ):

\frac{13}{20} \times \frac{5}{5} = \frac{65}{100}

Convert the fraction to a decimal by dividing the numerator by the denominator:

\frac{65}{100} = 0.65

Result: $\frac{13}{20}$ as a decimal is 0.65.

5. Converting a Fraction to a Percentage

infoNote

Example: Convert $\frac{5}{8}$ to a percentage.
Steps:

First, convert the fraction to a decimal by dividing the numerator by the denominator:

\frac{5}{8} = 0.625

Then, convert the decimal to a percentage by multiplying by $100$ :

0.625 \times 100 = 62.5\%

Result: $\frac{5}{8}$ as a percentage is 62.5%.

6. Converting a Percentage to a Fraction

infoNote

Example: Convert $12.5%$ to a fraction.
Steps:

Start by writing the percentage as a fraction over $100$ :

\frac{12.5}{100}

To remove the decimal, multiply both the numerator and the denominator by $10$ :

\frac{12.5 \times 10}{100 \times 10} = \frac{125}{1000}

Simplify the fraction by dividing both the numerator and the denominator by their GCD, which is $25$ :

\frac{125}{1000} = \frac{1}{8}

Result: $12.5%$ as a fraction is $\frac{1}{8}$ .

Fractions Simplified Revision Notes for GCSE OCR Maths

Fractions

Fraction of a Quantity

Equivalent Fractions

🔑 Key Rule:

Proper and Improper Fractions

Converting Improper Fractions to Mixed Numbers:

Converting Mixed Numbers to Improper Fractions:

Adding, Subtracting, Multiplying, and Dividing Fractions

(a) Adding and Subtracting Fractions

(b) Multiplying and Dividing Fractions

(c) Dividing Fractions:

Fractions, Decimals, and Percentages

Converting Between Fractions, Decimals, and Percentages:

500K+ Students Use These Powerful Tools to Master Fractions For their GCSE Exams.

Other Revision Notes related to Fractions you should explore