Pythagoras

1. What is Pythagoras' Theorem?

Pythagoras' Theorem is one of the most famous theorems in mathematics. It was "invented" by the Greek mathematician Pythagoras (or one of his loyal followers) around 600 BC. The theorem describes a very important relationship between the lengths of sides in a right-angled triangle:

Pythagoras' Theorem Statement: "If you take the lengths of the two shortest sides of any right-angled triangle, square them and add the answers together, you end up with the square of the longest side (the hypotenuse)."

Mathematically, this can be written as:

a^2+b^2=c^2

Where:

$a$ and $b$ are the lengths of the shorter sides of the triangle.
$c$ is the length of the hypotenuse (the longest side).

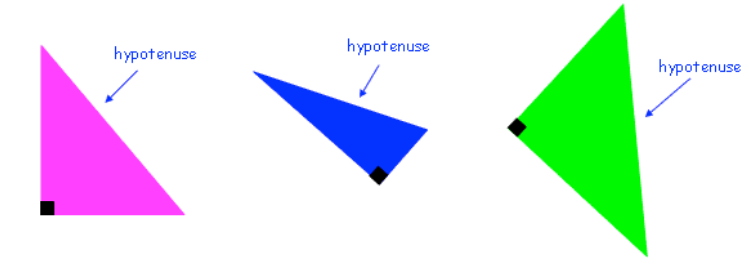
2. What is the Hypotenuse?

To effectively use Pythagoras' Theorem (and other trigonometry concepts), it is crucial to understand what the hypotenuse is in a right-angled triangle:

The hypotenuse is the longest side of a right-angled triangle.
It is always the side opposite the right angle.

3. The Two Forms of Pythagoras' Theorem

Pythagoras' Theorem can be rearranged depending on which side of the triangle you are solving for:

Finding the Hypotenuse:

c=\sqrt{a^2+b^2}

Use this formula when you know the lengths of both shorter sides ( $a$ and $b$ ) and need to find the hypotenuse ( $c$ ).

Finding a Shorter Side:

a=\sqrt{c^2−b^2}\quad or\quad b=\sqrt{c^2−a^2}

Use these formulas when you know the hypotenuse ( $c$ ) and one shorter side (either $a$ or $b$ ) and need to find the other shorter side.

4. Finding the Hypotenuse

When given the lengths of the two shorter sides of a right-angled triangle, you can find the length of the hypotenuse using Pythagoras' Theorem.

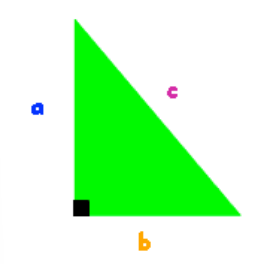
Steps to Find the Hypotenuse:

Label the Sides: Identify the hypotenuse $c$ , and label the other sides $a$ and $b$ .
Apply the Formula:

c^2=a^2+b^2

Substitute the Known Values: Replace a and b with the given numbers.
Solve for $c$ : Calculate $c^2$ , then take the square root to find $c$ .

infoNote

Example:

Question: A right-angled triangle has sides of 5 cm and 12 cm. Find the hypotenuse.
Solution:

c^2=5^2+12^2=25+144=169

c=\sqrt169=13 cm

Answer: The hypotenuse is 13 cm.

5. Finding a Side That Isn't the Hypotenuse

When given the hypotenuse and one of the shorter sides, you can find the other side using a rearranged version of Pythagoras' Theorem.

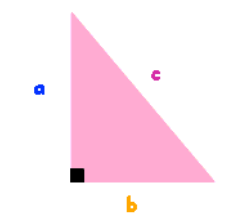
Steps to Find the Missing Side:

Label the Sides: Identify the hypotenuse $c$ , the side you need to find $a$ , and the other side $b$ .
Apply the Rearranged Formula:

a^2=b^2+c^2

Substitute the Known Values: Replace $c$ and $b$ with the given numbers.
Solve for $a$ : Calculate $a^2$ , then take the square root to find $a$ .

infoNote

Example:

Question: A right-angled triangle has a hypotenuse of 10 cm and one side of 6 cm. Find the other side.
Solution:

a^2=10^2−6^2=100−36=64

a=\sqrt64=8 cm

Answer: The missing side is 8 cm.

Worked Example: Finding the Hypotenuse

infoNote

Example

In this example, we are given the lengths of two sides of a right-angled triangle and need to find the length of the hypotenuse using Pythagoras' Theorem.

Steps to Solve:

Label the Sides:

$a=9 cm$ (one of the shorter sides)
$b=11 cm$ (the other shorter side)
$c=?$ (the hypotenuse, which is the side we need to find)

Apply the Pythagoras' Theorem:

c^2=a^2+b^2

Substituting the given values:

c^2=9^2+11^2

Calculate the Values:

c^2=81+121

c^2=202

Find the Hypotenuse: To find $c$ , we need to take the square root of both sides:

c=\sqrt202

c≈14.2\ cm(to\ 1\ decimal\ place)

Note: The hypotenuse c_c_ should always be the longest side of the triangle, and in this case, it is longer than both of the other sides, which is a good check that our calculations are correct.

Conclusion: The length of the hypotenuse $c$ is approximately 14.2 cm.

Worked Example: Finding a Side That Isn't the Hypotenuse

infoNote

Example We are given the length of the hypotenuse and one of the shorter sides of a right-angled triangle. We need to find the length of the other shorter side using Pythagoras' Theorem.

Steps to Solve:

Label the Sides:

$c=10.2 m$ (the hypotenuse)
$b=3.1 m$ (one of the shorter sides)
$a=?$ (the side we need to find)

Apply the Pythagoras' Theorem: Since we are not finding the hypotenuse, we use the rearranged formula:

a^2=c^2−b^2

Substituting the given values:

a^2=10.2^2−3.1^2

Calculate the Values:

a^2=104.04−9.61

a^2=94.43

Find the Side $a$ : To find a_a_, we need to take the square root of both sides:

a=\sqrt94.43

a≈9.72 m(to 2 decimal places)

Note: The side a_a_ is shorter than the hypotenuse $c$ , which is correct because the hypotenuse should always be the longest side of the triangle.

Conclusion: The length of the side $a$ is approximately 9.72 m.

Worked Example: Ladder Problem

infoNote

Example In this example, we have a ladder leaning against the side of a house. The problem is to find out how far up the side of the house the ladder reaches. This is a classic Pythagoras' Theorem problem where we need to find one side of a right-angled triangle when the other two sides are given.

Problem Statement: A 5m ladder rests against the side of a house. The foot of the ladder is 1.5m away from the house. How far up the side of the house does the ladder reach?

Steps to Solve:

Label the Sides:

$c=5$ m (the hypotenuse, which is the length of the ladder)
$b=1.5 m$ (the distance from the house to the foot of the ladder)
$a=?$ (the height we need to find)

Apply the Pythagoras' Theorem: Since we are not finding the hypotenuse, we use the rearranged formula:

a^2=c^2−b^2

Substituting the given values:

a^2=5^2−1.52

Calculate the Values:

a^2=25−2.25

a^2=22.75

Find the Side $a$ : To find a, we need to take the square root of both sides:

a=\sqrt22.75

a≈4.77 m(to 2 decimal places)

Note: The height $a$ is less than the length of the ladder $c$ , which makes sense because the hypotenuse is always the longest side in a right-angled triangle.

Conclusion: The ladder reaches approximately 4.77 m up the side of the house.

Worked Example: Finding the Distance Between Two Coordinates

infoNote

Example We are asked to find the distance between two points on a coordinate plane. This problem can be approached using Pythagoras' Theorem because the distance between the points forms the hypotenuse of a right-angled triangle.

Problem Statement: Find the distance between the coordinates (4,5) and (−2,1).

Steps to Solve:

Sketch the Coordinate Points:

Plot the points $(4,5)$ and $(−2,1)$ on a coordinate grid.
Draw a right-angled triangle by connecting these points with horizontal and vertical lines.

Label the Sides:

The horizontal distance ( $a$ ) between the points is $4−(−2)=6$ units.
The vertical distance ( $b$ ) between the points is $5−1=4$ units.
The hypotenuse ( $c$ ) is the distance we need to find.

Apply the Pythagoras' Theorem: To find the distance between the points, we use the Pythagoras' Theorem:

c^2=a^2+b^2

Substituting the known values:

c^2=6^2+4^2

Calculate the Values:

c^2=36+16

c^2=52

Find the Distance $c$ : To find $c$ , take the square root of both sides:

c=\sqrt52

c≈7.21 units(to 2 decimal places)

Conclusion: The distance between the points ( $4,5$ ) and ( $−2,1$ ) is approximately 7.21 units.

Pythagoras Simplified Revision Notes for GCSE OCR Maths

Pythagoras

1. What is Pythagoras' Theorem?

2. What is the Hypotenuse?

3. The Two Forms of Pythagoras' Theorem

4. Finding the Hypotenuse

5. Finding a Side That Isn't the Hypotenuse

Worked Example: Finding the Hypotenuse

Example

Worked Example: Finding a Side That Isn't the Hypotenuse

Worked Example: Ladder Problem

Worked Example: Finding the Distance Between Two Coordinates

500K+ Students Use These Powerful Tools to Master Pythagoras For their GCSE Exams.

Other Revision Notes related to Pythagoras you should explore