Volume

What is a Prism?

Definition:

A prism is a 3D object where the cross-section (the shape you see if you cut straight through it) remains the same along the entire length of the object.

In simpler terms, if you were to slice the prism perpendicular to its length, every slice would look exactly the same.

infoNote

Examples of Prisms:

A cuboid (a box shape) is a prism because every cross-section parallel to its base is a rectangle of the same size.
A cylinder is also a prism because every cross-section parallel to its circular base is a circle of the same size. Non-Examples:
A pyramid is not a prism because as you move from the base to the apex, the cross-section changes size.
A cone is also not a prism for the same reason.

Working Out the Volume of a Prism

Formula:

Volume of a Prism=Area of Repeating Face×Length

The repeating face is the $2D$ shape that, when extended or extruded along the length, creates the $3D$ prism.
The length (or height, depending on the orientation of the prism) is how far the shape extends in the third dimension.

infoNote

Example 1: Volume of a Cuboid

Problem: Calculate the volume of a cuboid with a base measuring 8 cm by 5 cm and a height of 4 cm.

Solution:

Step 1: Calculate the Area of the Repeating Face

The repeating face of this cuboid is a rectangle.
Dimensions of the rectangle: Base $b=8 cm$ , Height $h=5 cm.$ Formula for the Area of a Rectangle:

Area=b×h

Substitute the values:

Area=8 \ cm×5 \ cm=40 \ cm^2

The area of the repeating face is 40 cm².

Step 2: Multiply by the Length (or Height) of the Prism

The length of the cuboid is 4 cm. Formula for the Volume of the Prism:

Volume=Area of Repeating Face×Length

Substitute the values:

Volume=40 \ cm^2×4 \ cm=160 \ cm^3

The volume of the cuboid is 160 cm³.

Volume of a Triangular Prism

Key Formula:

Volume of a Prism=Area of Repeating Face (Cross-Section)×Length

The repeating face or cross-section of a triangular prism is a triangle.
The length (or height) of the prism is the distance the triangular face is extruded along.

infoNote

Example 2: Triangular Prism

Problem: Calculate the volume of a triangular prism where the base of the triangular face is 6m, the height of the triangular face is 11m, and the length of the prism is 5m. Note that an additional measurement of 15m is given, but this is not needed for the volume calculation.

Solution:

Step 1: Calculate the Area of the Repeating Face (Triangle)

Dimensions of the triangle:
Base $b=6 m$
Height $h=11 m$

Formula for the Area of a Triangle:

Area=\frac{b×h}2

Substitute the values:

Area=\frac{6 \ m×11 \ m}2=\frac{66 \ m^2}2=33 \ m^2

The area of the triangular face is 33 m².

Step 2: Multiply by the Length of the Prism

The length of the prism is 5 m. Formula for the Volume of the Prism:

Volume=Area of Repeating Face×Length

Substitute the values:

Volume=33 \ m^2×5 \ m=165 \ m^3

The volume of the triangular prism is 165 m³.

infoNote

Example 3: Volume of a Cylinder

Problem: Calculate the volume of a cylinder with a radius of 3mm and a height of 6.2mm.

Solution:

Step 1: Calculate the Area of the Repeating Face (Circle)

Given:
Radius $r=3 mm$ Formula for the Area of a Circle:

Area=π×r^2

Substitute the values:

Area=π×3^2=π×9≈28.274 \ mm^2

The area of the circular face is approximately 28.274 mm².

Note: Keep this value in your calculator to maintain accuracy for the next calculation.

Step 2: Multiply by the Height of the Cylinder

Given:
Height $h=6.2 mm$ Formula for the Volume of the Cylinder:

Volume=Area of Repeating Face×Height

Substitute the values:

Volume=28.274 \ mm^2×6.2 \ mm≈175.3 \ mm^3

The volume of the cylinder is approximately 175.3 mm³ (rounded to 1 decimal place).

infoNote

Example 4: Complicated Prism

Problem: Calculate the volume of a prism where the cross-sectional face is a rectangle with a circular hole in it. The rectangle has a base of 5m, a height of 7m, and the circular hole has a radius of 1.5m. The length of the prism is 3m.

Solution:

Step 1: Calculate the Area of the Complete Rectangle (Ignoring the Hole)

Dimensions of the rectangle:
Base $b=5 m$
Height $h=7 m$ Formula for the Area of a Rectangle:

Area=b×h

Substitute the values:

Area=5 \ m×7 \ m=35 \ m^2

Step 2: Calculate the Area of the Circular Hole

Radius of the circle: $r=1.5 m$ Formula for the Area of a Circle:

Area=π×r^2

Substitute the values:

Area=π×(1.5 \ m)^2=π×2.25 \ m^2≈7.068 \ m^2

Step 3: Subtract the Area of the Circular Hole from the Area of the Rectangle

Area of Repeating Face:

Area of Repeating Face=Area of Rectangle−Area of Circle

Substitute the values:

Area\ of\ Repeating\ Face=35\ m^2−7.068 \ m^2=27.931 \ m^2

Step 4: Multiply by the Length of the Prism

Length of the prism: 3 m Formula for the Volume of the Prism:

Volume=Area of Repeating Face×Length

Substitute the values:

Volume=27.931 \ m^2×3 \ m=83.793 \ m^3

Round to one decimal place:

Volume≈:success[83.8 m³]

Volume of Pointed Shapes

Key Formula:

\text{Volume of a Pointy Shape}=\frac{\text{Area of Base}×Height}3

The area of the base is the area of the flat face (usually a circle for cones or a polygon for pyramids).
The height is the perpendicular distance from the base to the point (the apex) of the shape.

infoNote

Example 4: Volume of a Cone

Problem: Calculate the volume of a cone with a base radius of 90 m and a height of 50m.

Solution:

Step 1: Calculate the Area of the Base (Circle)

Given:
Radius $r=90 m$

Formula for the Area of a Circle:

Area=π×r^2

Substitute the values:

Area=π×(90 \ m)^2=π×8100 \ m^2≈25,446.9 \ m^2

The area of the circular base is approximately 25,446.9 m².

Step 2: Use the Volume Formula for a Cone

Height of the cone: 50 m Formula for the Volume of a Cone:

Volume=\frac{Area\ of\ Base×Height}3

Substitute the values:

                    $Volume=\frac{25,446.9\  m^2×50 \ m}3=\frac{1,272,345 \ m^3}3≈424,115 \ m^3$

Round to the nearest whole number:

Volume≈:success[424,115 m³]

Volume of a Sphere

Key Formula:

Volume of a Sphere= $\frac{4}3×π×r^3$

$r$ is the radius of the sphere.
$π$ (pi) is approximately 3.14159.

infoNote

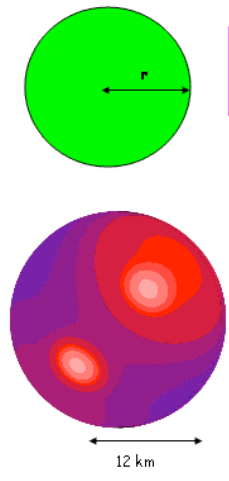
Example 5: Volume of a Sphere

Problem: Calculate the volume of a sphere with a radius of 12 km.

Solution:

Step 1: Write Down the Formula

Volume\ of\ a\ Sphere=\frac{4}3×π×r^3

Step 2: Substitute the Radius into the Formula

Given: $r=12 km$
Substitute the value of $r$ into the formula:

Volume=\frac{4}3×π×(12)^3

Step 3: Calculate the Cube of the Radius

Calculate $12^3$ :

12^3=12×12×12=1,728 \ km^3

Step 4: Multiply by ππ and Then by $\frac{4}3$

Multiply by $π$ :

π×1,728≈3.14159×1,728=5,429.63 \ km^3

Now, multiply by $\frac{4}3$ :

Volume=\frac{4}3×5,429.63≈7,238.29 \ km^3

Step 5: Final Answer

The volume of the sphere is approximately 7,238.29 km³.

Volume Simplified Revision Notes for GCSE OCR Maths

Volume

What is a Prism?

Definition:

Working Out the Volume of a Prism

Example 1: Volume of a Cuboid

Volume of a Triangular Prism

Example 2: Triangular Prism

Example 3: Volume of a Cylinder

Example 4: Complicated Prism

Volume of Pointed Shapes

Example 4: Volume of a Cone

Volume of a Sphere

Example 5: Volume of a Sphere

500K+ Students Use These Powerful Tools to Master Volume For their GCSE Exams.

Other Revision Notes related to Volume you should explore