Coordinate Geometry: The Circle

Equation of a Circle

• The equation of the circle with centre (0,0) and radius r is: $x^2 + y^2 = r^2$

• The equation of the circle with centre (h,k) and radius r is: $(x-h)^2 + (y-k)^2 = r^2$

• To find where circle intersects the x-axis and y-axis:

  • Let y=0 and solve for x to find x-intercepts
  • Let x=0 and solve for y to find y-intercepts

• The equation $x^2+y^2+2gx+2fy+c=0$ represents a circle with:

  • Center = (-g,-f)
  • Radius = $\sqrt{g^2+f^2-c}$

• If (x,y₁) lies (i) Inside Circle $(x_1-h)^2+(y_1-k)^2 < r^2$

  • (ii) Outside Circle $(x_1-h)^2+(y_1-k)^2 > r^2$
  • (iii) On the Circle $(x_1-h)^2+(y_1-k)^2 = r^2$

• If (x1y1) lies (i) Inside Circle $x_1^2+y_1^2+2gx_1+2fy_1+c < 0$

  • (ii) Outside Circle $x_1^2+y_1^2+2gx_1+2fy_1+c > 0$
  • (iii) On the Circle $x_1^2+y_1^2+2gx_1+2fy_1+c = 0$

Find intersection of a line and a Circle

• Can intersect at two points, one point (tangent) or not at all
• Always substitute from linear equation into circle equation

Locus - path traced out by a moving point satisfying certain given conditions

---

Coordinate Geometry : The Circle

Tangents and Circles

• To get the equation of the tangent to a point on a circle :

  • Find slope of radius
  • Find slope of tangent
  • Use point on circle to find equation

• To get equation of tangent from outside a circle :

  • Find centre and radius of circle
  • Let slope of tangent be m
  • Write equation of tangent in m in the form ax+by+c=0
  • Find in terms of m the distance from tangent to centre of the circle and set this equal to the radius length. - Solve for m
  • Rewrite Equation using value for m

Tangents and Circles

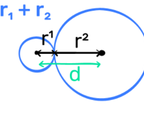
If two circles touch externally: d = r₁ + r₂

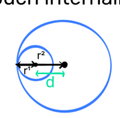
If two circles touch internally: d = r₁ - r₂

Common chord - Common tangent

• For circles s1 and s2 expressed in form x²+y²+2gx+2fy+c=s₁-s₂ = 0 is the equation of the common chord / tangent

Circles touching the x-axis or y-axis

If circle x²+y²+2gx+2fy+c = 0 (i) touches x-axis then g²=c and radius = |-f| (ii) touches y-axis then f²=c and radius = |-g|