ALGEBRA 1

Algebraic Expressions

• A variable is a letter that represents a number.
• A coefficient is a number or symbol that is multiplying a variable.
• A constant is a quantity that does not change in value.
• An algebraic expression is an expression containing one or more numbers, one or more variables, and one or more arithmetic operations.
• Polynomials have variables that have only non-negative whole number powers.
• A polynomial in x has the form:

$a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_2x^2+a_1x^1+a_1$

where all coefficients $a_n,a_{n-1},a_{n-2},...,a_2,a_1$ are constants and the powers are non-negative whole numbers.

• The degree of the polynomial is equal to the highest power.

Addition/Subtraction

• Like terms are terms with the exact same letters raised to the same power the powers are non-negative whole numbers.
• Adding or subtracting like terms-powers of variables do not change but coefficients do.

Multiplying

• Multiplying coefficient x coefficient, variable x variable
• Remember $a^ma^n = a^{m+n}$

---

Important Products

x(y+z) = xy+xz
(a+b)(x+y) = ax+ay+bx+by
(a+b)(a-b) = a²-b²
(a+b)² = a²+2ab+b²

• (a-b)² = a²-2ab+b²
• (a+b)³ = a³+3a²b+3ab²+b³
• (a-b)³ = a³-3a²b+3ab²-b³

Pascal's Triangle

• When faced with a binomial expansion such as (a+b)⁵ the expansion looks like this

a⁵b⁰+5a⁴b¹+10a³b²+10a²b³+5a¹b⁴+a⁰b⁵

• NB Notice the first term is a⁵ and then the power of a decrease by 1 each term eventually reaching 0.
• The powers of b start at 0 and increase by 1 each term.
• The coefficients in the expansion can be found in Pascal's triangle on one row further than the highest power of expansion.
• For example : Row 6. 1, 5, 10, 10, 5, 1 as above

Factorising

• Four Methods

  • Highest Common Factor
  • Grouping
  • Difference of Two Squares
  • Quadratic Trinomials

• Factorising cubic expressions:

---

Algebraic Fractions

To add/subtract algebraic fractions - find the lowest common denominator

Multiplying Fractions ➡ $\frac{\text{numerator} \times \text{numerator}}{\text{denominator} \times \text{denominator}}$

Dividing Fractions ➡ Multiply by the reciprocal of the divisor.

Binomial Expansions

Binomial expansions is where an expression is multiplied by itself many items

• The (r+1)th term, $T_{r+1}$ of the binomial expansion of $(x+y)^n$ is given by:

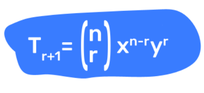
• This is the general term.
• The middle term of an expansion is found as such:

-The number of terms in an expansion is $n+1$

-So find middle term of $n+1$ and that is equal to $T_{r+1}$

---

Finding the term of a binomial expansion Independent of x

• This means finding the constant when $x^n$

Long division in Algebra

• Numerator is called the dividend
• Denominator is called the divisor
• A remainder of 0 means the divisor is a factor of the dividend.
• A quotient is the result of division

---

ALGEBRA 2

Solving Linear Equations

• There are three ways to solve Linear equations:

  • Algebra
  • Using trial and error
  • Graphing

• Methods of solving simultaneous Linear equations (two variables)

  • Using trial and error
  • Graphs - Find point of intersection
  • Elimination
  • Substitution

• Steps to solve simultaneous equations (three variables)

  • Select one variable and eliminate it from a pair of equations
  • Now with two equations and two unknowns eliminate one more variable

Solving Quadratic Equations

• Graphing
• Algebra
• Quadratic Formula

$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$

a = coefficient of x² b = coefficient of x c = constant term

• When given the roots change them into factors and multiply
• If coefficient of x² is 1:

Quadratic x² - (Sum of roots)x + (Product of roots) = 0

---

Simultaneous Equations - One linear and One Non-Linear

• Always substitute from the linear into the non-linear
• Always substitute back into the linear. This will avoid obtaining an incorrect solution.

The Factor Theorem

• A polynomial f(x) has a factor (x-a) if and only if f(a)=0
• A polynomial f(x) has a factor (x-a) if and only if its graph touches or crosses the x-axis at x=a (a cR)

More about graphs:

• The values for x for which f(x)=0 are called roots or zeros
• The degree of polynomial is the highest power within the polynomial
• The max number of distinct roots a polynomial can have is the same as it's degree
• The leading coefficient is the coefficient of the term with the highest power
• If a root has an even multiplicity - touching
• If a root has an odd multiplicity - Crossing
• Even degree - arms of graph both point up or down
• Odd degree - arms of graph point in different directions
• Right arm points up if leading coefficient is positive
• Right arm points down if leading coefficient is negative
• NB many polynomials can have the same roots so when finding a polynomial expression it is a possible answer

Unknown Coefficients

'It is true for all values of xcR' means the LHS = RHS

---

ALGEBRA 3

Surds Equations

• A number of the form $\pm\sqrt{a}$ where $a$ is a positive rational number that is not the square of another rational number, is called a pure quadratic surd. A number of the form $a\pm\sqrt{b}$, where $a$ is rational and $\sqrt{b}$ is a pure quadratic surd, is sometimes called a mixed quadratic surd.

• Square both sides of equations to eliminate square root.

• Is necessary to check any solution because squaring can introduce an erroneous solution ➜ check into original equation.

Linear Inequalities

• An inequality gives a range of values.

Less than | greater than | less than or equal to | greater then or equal to

• When multiplying or dividing by a negative number - reverse the inequality sign, as well as changing the signs of all terms in the inequality.

Quadratic and rational inequalities

means 'below the x-axis' | means 'above the x-axis' | means 'on or below the x-axis' | means 'on or above the x-axis'

---

ALGEBRA 3

• Rational inequalities - cannot be sure if denominator is positive/negative
• To solve - multiply both sides by (denominator)² which we know is positive.

Absolute Value (Modulus)

• The absolute value of a real number x written as |x|, is the magnitude of the number without regard to its sign (i.e. non-negative value of the number).
  If x < 0, |x| = -x if x ≥ 0, |x| = x.

• When x ≥ 0 and |x| = a then x = -a or x = a

• Squaring a modulus removes it's modulus notation.

• Notice the graph of y = |x| is a combination of the graph of y=-x on x < 0 x∈R and the graph of y = x on x ≥ 0, x∈R

• For modulus inequalities:

  • If |x| < a, then -a < x < a, where a > 0, a∈R
  • If |x| > a, then x < -a, or x > a, where a > 0, a∈R

Proof for inequalities

• (real)² ≥ 0

Disriminants for proofs

• Real roots → b² - 4ac ≥ 0
• Real and distinct roots → b² - 4ac > 0
• Real and equal roots → b² - 4ac = 0
• No real roots → b² - 4ac < 0