Photo AI
Last Updated Sep 26, 2025
Sets and Functions Simplified Revision Notes for Scottish Highers Maths
Revision notes with simplified explanations to understand Sets and Functions quickly and effectively.
322+ students studying
Functions
- A function is a rule that maps an input to a unique output
- An input is an object that is put into the function
- The domain is the set of all inputs for which a function is defined
- An output is the object that comes out of the function
- The range is the set of actual output values of a function
- The codomain is the set of all possible output values of a function
Representing the rule for a function

| f(x) = x² | f→x² | f = {(−1,1),(0,0),(1,1),(2,4)} |
|---|---|---|
| f of x equals x- squared | f maps x to x² | Ex : if 2 is input, 4 is output |
Identify a function
- An input into a function will never result in two different outputs
- We can use the vertical line test to determine if the mapping is a function or not
- Should cut graph at only one point.
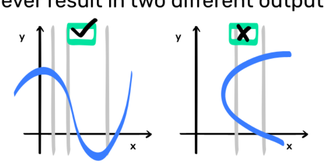
Functions as mappings from one set to Another
- N - Natural Numbers
- Z - Integers
- Z⁺ - Positive Integers
- R - Real numbers
- R⁺ - Positive real numbers
- Q - Rational numbers
- Q⁺ - Positive rational numbers
Functions
Intervals
- [a,b] = {x∈R|a ≤ x ≤ b} - closed interval, a value and b value are included
- (a,b)= {x∈R|a < x < b} - open interval, a value and b value are not included
- [a,b) = {x∈R|a ≤ x ≤ b} - a value included but b value not included
- (a,b] = {x∈R|a < x ≤ b} - a value not included but b value included
Examples:
f: N→N : x→2x
- Domain: N
- Codomain: N
- For this function range consists of even natural numbers only
- Note: Range and codomain are different sets.
f: R→R : x→x²
- Domain: R
- Codomain: R
- Range: [0,∞] (zero included f(0)=0)
- Note: ∞ is not included as is not a finite number
Composite Functions
- Functions can often be broken up
- Consider function p given by p(x) = 3x² + 5
- We can understand this type of function easier if we break up into two separate functions g and h
- The function g is defined as g(x) = x² x∈R
- The function h is defined as h(x) = 3x + 5 x∈R
- We want to find g(x) first then use g(x) as the input for the function h(x)
- If we perform function g first and then h, we express this as :
h∘g(x) or (h∘g)(x) or h(g(x)) or hg(x)
Functions

- In general composition of functions is not commutative.
ie · f·g(x) ≠ g·f(x)
Linear and Quadratic Functions and Transformations
- Linear Function - f in x is a function of the form f(x) = ax+b, where a and b are constants and x is a variable
- If we add a number to the function it shifts up or down
- If we change the slope or coefficient of x the steepness changes
- Quadratic function - f in x involves an x² term and is of the form f(x) = ax² + bx + c, where a, b, and c are constants and x is a variable
- When we transform a quadratic function the graph can
- Narrow - for quadratic function f(x) = ax², a>0, as the value of a increases, the graph of y=f(x) becomes narrower
- Shift up or down -
- If b is positive the graph of f(x) = x²+b is the graph of y=x² shifted b units upwards.
- If b is negative the graph of f(x)=x²+b is the graph of y=x² shifted -b units downward
Shift left or right
- If b is positive, the graph of f(x)=(x+b)² is the graph of y=x² shifted b units to the left. If b is negative, the graph of f(x)=(x+b)² is the graph of y=x² shifted -b units to the right. The y-intercept of the function f(x)=(x+b)² is (0, (b)²)
Quadratic Functions and completed Square Form
- Turning point of function = vertex
- Completing the square is the method of converting from standard form (ax²+bx+c) to completed square form (a(x-h)²+k). (h,k) are the coordinates of the vertex of the function. The axis of symmetry for the graph of f is x.

y = a(x-h)²+k
a>0 U shaped a<0 ∩ shaped
vertex h, k axis of summetry x = h
Steps for completing the square
-
Put ax² + bx + c in the form a(x² + x + )
-
Halve the coefficient of x and put it in bracets ...a[(x + ())² +...
-
Subtract half the coefficient of x squared and include
a[(x + ())² - (())² + ]
-
Evaluate and simplify then multiply by a
Cubic Functions
-
A cubic function - f in x involves an x³ term and is of the form f(x) = ax³ + bx² + cx + d where a, b, c and d are constants (a≠0) and x is a variable
-
If coefficient of x³ is positive - graph starts low, ends high
-
If coefficient of x³ is negative - graph starts high, ends low
Transforming a cubic function:
- Adding a number to the function shifts graph up y-axis
- Subtracting a number from function shifts graph down y-axis
- Multiplying a function by a number, the effect is compression or elongation.
- multiply by 0.5 - graph is compressed by factor of (0.5) each y - value is halved
- multiply by 2 - graph is longer by factor of 2 - each y-value doubles
- Multiplying by a number does not affect the roots
Exponential Functions
- Exponential Functions are functions of the form y = bˣ, where b is constant and x is the variable exponent or power

-
Note: Graph of function f(x)=abˣ will pass through point (0,a) (At x=0, y=ab⁰ =a(1) = a )
-
Graph of exponential function will never touch or cross horizontal axis
-
If exponent is x and the base is greater than 1, curve slopes upwards
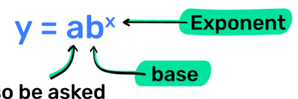
Functions

- If exponent is x and the base is positive but less than 1, curve slopes down
- Note : is the same as or
- The graph of f(x)=k× is the graph of y=k× shifted h units to the left if h > 0 or -h units to the right if h < 0
Graphing Logarithmic Functions
- All exponential functions have inverse functions called Logarithmic Functions
- Exponential and logarithmic functions are symmetric to each other across the line y = x
Transformations: y = a log (x±b)±c
-
Multiplying by a does not affect roots only compresses or elongates function. (Ex multiplying by 0.5 = all y values halved) (compared to original)
-
-b - shift b units to right ● +b - shift b units to left
-
+c - shift c units up ● -c - shift c units down
Injective, Surjective and Bijective Functions
- Injective function (one - to - one) - never assigns the same output value to two different input values
- The function f is injective if ∀ a, b ∈ A, whenever f(a)=f(b) then a=b (Note ∀ means for all/any)
Functions

-
Horizontal line test for Injectivity- If the horizontal axis, is the input axis, then, if any horizontal line cuts the graph of function at no more than one point function is injective
-
Test by algebra - Take values of ∈R a, b and let f(a) = f(b)
-
Surjective function (onto) - a function which every element in the codomain has at least one matching element in the domain.
-
Codomain = Range
-
The function f is surjective if ∀ b∈B, ∃ a ∈A such that f(a)=b (∃ "there exists")
-
Horizontal Line test for surjectivity - if f is surjective then every horizontal line y=b where b ∈ B, intersects graph of f at least one point.
-
Algebraically -
- Rearrange y = f(x) and express y in terms of x
- If expression for x in terms of y makes sense (a real number) for all y then function is surjective
-
Bijective function - a function f is said to be bijective if it is both injective and surjective
-
To change a function to be bijective:
- Restrict domain so what remains is injective
- Restrict codomain so what remains is surjective.
Inverse Functions
-
If two functions f and g are defined so that f: A→ B and g: B→ A, then, if (f·g) (x) = (g·f) (x) = x we say that f and g are inverse functions of each other
-
A function f has an inverse function f⁻¹ if and only if f is bijective
-
A function f that is bijective will have a unique inverse function f⁻¹
Functions
- A function cannot have more than one inverse.
- Note how important domain and codomain are in determining if a function is invertible
- Also remember h : R→R* : x→ex so h-1: R* → R : x→/nx
Steps to find inverse with example
1. Let f(x) = y 1. y = 2x+3 , x ∈ R
2. Express x in terms of y 2. y-3 = 2x ⇒ x = y-3/2
3. Rewrite as f-1(x) replacing 3. f-1(x) = x-3/2 , x ∈ R y with x
Graphs of Inverse Functions
-
For any invertible function f and its inverse f-1, we get the following: If (c,d) is a point on graph of f, then (d,c) is point on graph of f-1 point on graph of f-1 graphs of f and f-1 are reflections of each other about line y = x
-
Remember: cos𝜃 = x - coordinate sin𝜃 = y - coordinate
-
Period - the horizontal distance required for the graph to complete one cycle
-
Range - the set of all actual outputs of the function
-
Amplitude - the number of units the graph goes up or down from the midline of the graph
-
Frequency - Number of waves that pass fixed point in a given amount of time

Functions

- Asymptote - a line which the curve will approach but never meet.
sin Function y = sinθ
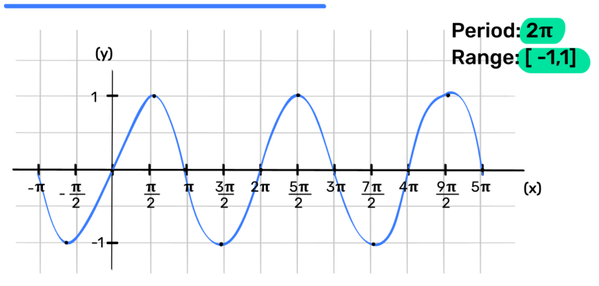
Period: 2π Range: [-1,1]
- *The graph repeats itself every 2π radians, so it is a periodic function
cos Function y = cosθ
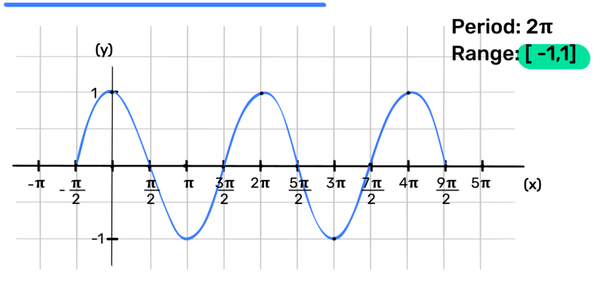
Period: 2π Range: [-1,1]
Functions
Tan Function y = tan𝜃

Period: π Range: (-∞, ∞)
- There are asymptotes at 𝜃 = ± , ± , ± , ...*(at all odd multiples of radians
To Note: If a, n ∈ N then :
- a sin𝜃 has period and range [-a,a]
- a casn𝜃 has period and range [-a,a]
- a tann𝜃 has period and range [-∞,∞]
ie : Sin𝜃 and Cos c𝜃 Period = have
Composite Functions
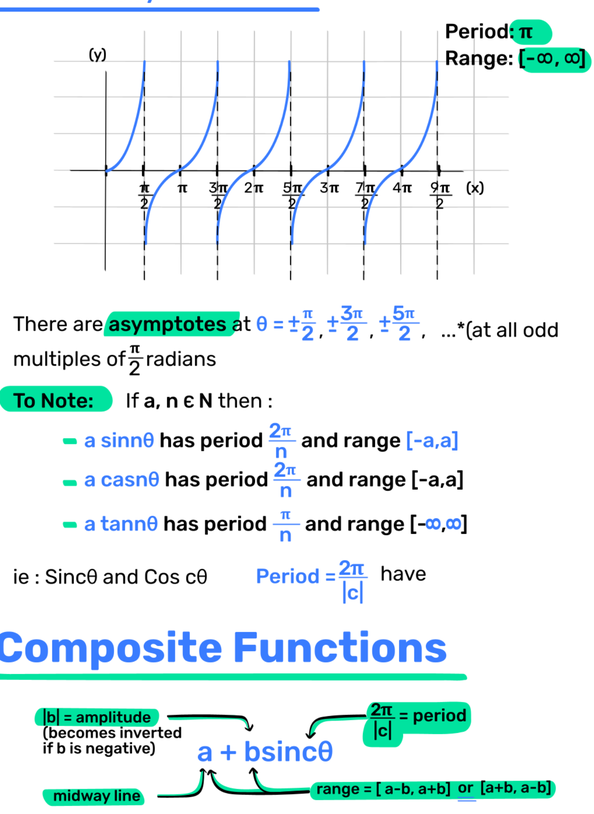
|b| = amplitude (becomes inverted if b is negative) → = period
a + bsin𝜃
midway line → range = [a-b, a+b] or [a+b, a-b]
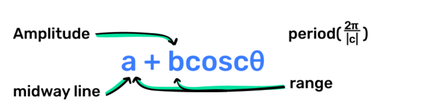
Amplitude → period()
a + bcos𝜃
midway line → range
Functions

- If a number is added or subtracted inside with x then it moves along the x axis like normal functions
Ex:
This is the graph of sin x shifted to the right
Inverse Functions
- Only functions that are bijections can have an inverse function.
- Ex: Sine function is not bijective unless we restrict the domain and range.
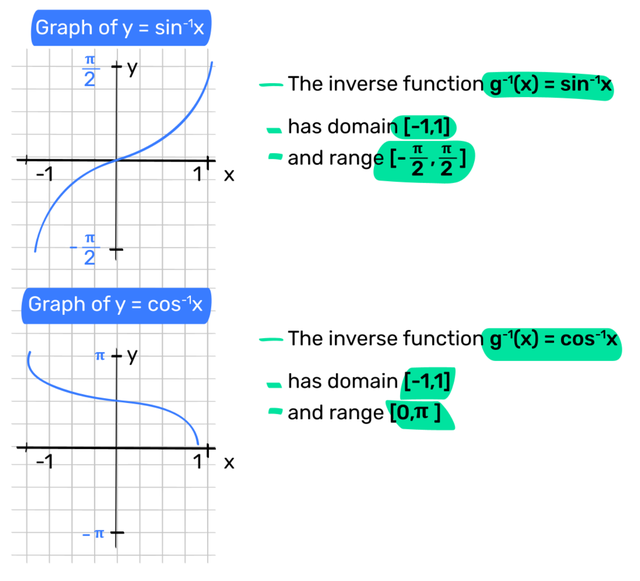
Graph of y = sin⁻¹x
- The inverse function g⁻¹(x) = sin⁻¹x
- has domain [-1,1]
- and range [-π/2, π/2]
Graph of y = cos⁻¹x
- The inverse function g⁻¹(x) = cos⁻¹x
- has domain [-1,1]
- and range [0,π]
Functions

The inverse function g⁻¹(x) = tan⁻¹x
- has domain (-∞,∞)
- and range (-π/2, π/2)
• The ranges of the inverse trigonometric functions are known as principal values. When we use calculator to find the inverse trigonometric functions the answer will always be within the range of principal values
| Trig Ratio | Principal Values |
|---|---|
| sin⁻¹ | -90° ≤ θ ≤ 90° or -π/2 ≤ θ ≤ π/2 |
| cos⁻¹ | 0° ≤ θ ≤180° or 0 ≤ θ ≤ π |
| tan⁻¹ | -90° < θ < 90° or -π/2 ≤ θ ≤ π/2 |

500K+ Students Use These Powerful Tools to Master Sets and Functions For their Scottish Highers Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
20 flashcards
Flashcards on Sets and Functions
Revise key concepts with interactive flashcards.
Try Maths Flashcards2 quizzes
Quizzes on Sets and Functions
Test your knowledge with fun and engaging quizzes.
Try Maths Quizzes13 questions
Exam questions on Sets and Functions
Boost your confidence with real exam questions.
Try Maths Questions3 exams created
Exam Builder on Sets and Functions
Create custom exams across topics for better practice!
Try Maths exam builder15 papers
Past Papers on Sets and Functions
Practice past papers to reinforce exam experience.
Try Maths Past PapersOther Revision Notes related to Sets and Functions you should explore
Discover More Revision Notes Related to Sets and Functions to Deepen Your Understanding and Improve Your Mastery
Load more notes