Photo AI

Given that $a$ is a constant, prove by mathematical induction that, for every positive integer $n$, $$\frac{d^n}{dx^n}(xe^{ax}) = n a^{n-1} e^{ax} + a^n x e^{ax}.$$ - CIE - A-Level Further Maths - Question 3 - 2015 - Paper 1

Question 3

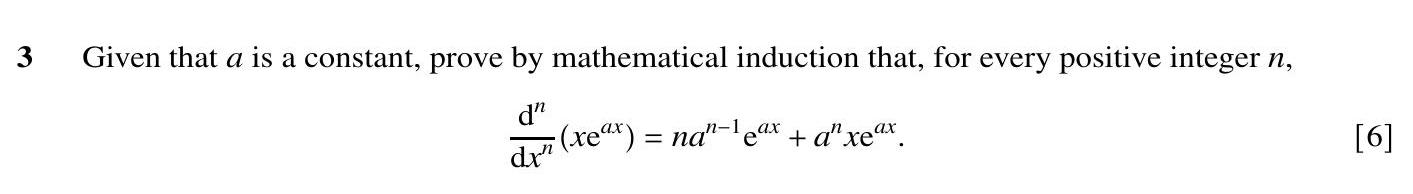
$Given-that-$a$-is-a-constant,-prove-by-mathematical-induction-that,-for-every-positive-integer-$n$,---$$\frac{d^n}{dx^n}(xe^{ax})-=-n-a^{n-1}-e^{ax}-+-a^n-x-e^{ax}.$$-CIE-A-Level Further Maths-Question 3-2015-Paper 1.png$

Given that $a$ is a constant, prove by mathematical induction that, for every positive integer $n$, $$\frac{d^n}{dx^n}(xe^{ax}) = n a^{n-1} e^{ax} + a^n x e^{ax}.$... show full transcript

Worked Solution & Example Answer:Given that $a$ is a constant, prove by mathematical induction that, for every positive integer $n$, $$\frac{d^n}{dx^n}(xe^{ax}) = n a^{n-1} e^{ax} + a^n x e^{ax}.$$ - CIE - A-Level Further Maths - Question 3 - 2015 - Paper 1

Step 1

Base Case: $n = 1$

96%

114 rated

Answer

To establish the base case, we calculate:

$\frac{d}{dx}(xe^{ax}) = e^{ax} + ax e^{ax}.$
This matches the formula for $n=1$ : $1 a^{1-1} e^{ax} + a^1 x e^{ax} = e^{ax} + ax e^{ax}.$
Thus, the base case holds.

Step 2

Induction Hypothesis: Assume $H_k$ is true

99%

104 rated

Answer

Assume that the statement holds for some integer $k$ , i.e.,
$\frac{d^k}{dx^k}(xe^{ax}) = k a^{k-1} e^{ax} + a^k x e^{ax}.$

Step 3

Induction Step: Prove for $n = k + 1$

96%

101 rated

Answer

We need to show that: $\frac{d^{k+1}}{dx^{k+1}}(xe^{ax}) = (k+1) a^k e^{ax} + a^{k+1} x e^{ax}.$
Using the product rule on our induction hypothesis, we compute:

$\frac{d^{k+1}}{dx^{k+1}}(xe^{ax}) = \frac{d}{dx}\left(\frac{d^k}{dx^k}(xe^{ax})\right) = \frac{d}{dx}\left(k a^{k-1} e^{ax} + a^k x e^{ax}\right).$
Applying the derivative:

$= k a^{k-1} a e^{ax} + a^k e^{ax} + a^k x a e^{ax} = (k a^k + a^k) e^{ax} + a^{k+1} x e^{ax} = (k+1) a^k e^{ax} + a^{k+1} x e^{ax}.$
This proves the statement for $n = k + 1$ .

Step 4

Conclusion

98%

120 rated

Answer

By the principle of mathematical induction, since the base case holds and the induction step is verified, we conclude that: $\frac{d^n}{dx^n}(xe^{ax}) = n a^{n-1} e^{ax} + a^n x e^{ax}$
is true for all positive integers $n$ .

Join the A-Level students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

Given that $a$ is a constant, prove by mathematical induction that, for every positive integer $n$, $$\frac{d^n}{dx^n}(xe^{ax}) = n a^{n-1} e^{ax} + a^n x e^{ax}.$$ - CIE - A-Level Further Maths - Question 3 - 2015 - Paper 1

Worked Solution & Example Answer:Given that $a$ is a constant, prove by mathematical induction that, for every positive integer $n$, $$\frac{d^n}{dx^n}(xe^{ax}) = n a^{n-1} e^{ax} + a^n x e^{ax}.$$ - CIE - A-Level Further Maths - Question 3 - 2015 - Paper 1

Base Case: $n = 1$

Induction Hypothesis: Assume $H_k$ is true

Induction Step: Prove for $n = k + 1$

Conclusion

Join the A-Level students using SimpleStudy...

Other A-Level Further Maths topics to explore