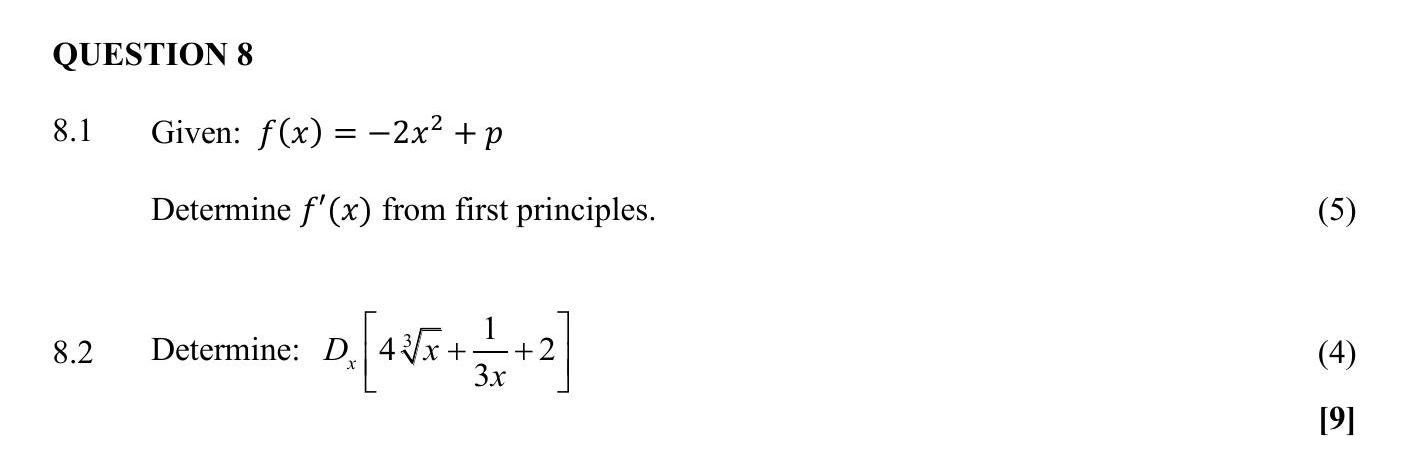Photo AI

8.1 Given: $f(x) = -2x^2 + p$ Determine $f'(x)$ from first principles - NSC Mathematics - Question 8 - 2017 - Paper 1

Question 8

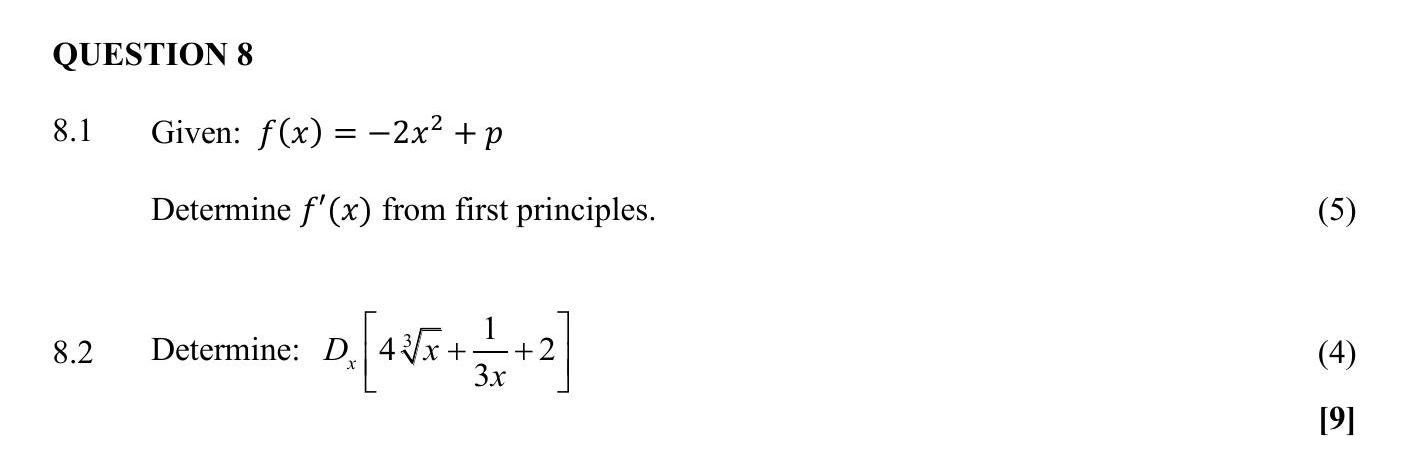
8.1 Given: $f(x) = -2x^2 + p$ Determine $f'(x)$ from first principles. 8.2 Determine: $D_x \left[ 4\sqrt{x} + \frac{1}{3x^2} + 2 \right]$

Worked Solution & Example Answer:8.1 Given: $f(x) = -2x^2 + p$ Determine $f'(x)$ from first principles - NSC Mathematics - Question 8 - 2017 - Paper 1

Step 1

96%

114 rated

Answer

To determine the derivative $f'(x)$ from first principles, we use the definition of the derivative:

$f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$

Substitute $f(x)$ into the formula: $f'(x) = \lim_{h \to 0} \frac{(-2(x + h)^2 + p) - (-2x^2 + p)}{h}$
Expand $(-2(x + h)^2 + p)$ : $(-2(x^2 + 2xh + h^2) + p) - (-2x^2 + p)$
Simplifying results in: $= \lim_{h \to 0} \frac{(-2x^2 - 4xh - 2h^2 + p) - (-2x^2 + p)}{h}$ $= \lim_{h \to 0} \frac{-4xh - 2h^2}{h}$
Factor out $h$ to simplify: $= \lim_{h \to 0} (-4x - 2h)$
As $h$ approaches zero, the limit becomes: $f'(x) = -4x$

Step 2

99%

104 rated

Answer

To find the derivative of the function $D_x \left[ 4\sqrt{x} + \frac{1}{3x^2} + 2 \right]$ , we will differentiate each term separately:

Derivative of $4\sqrt{x}$ : $D_x[4\sqrt{x}] = 4 \cdot \frac{1}{2\sqrt{x}} = \frac{2}{\sqrt{x}}$
Derivative of $\frac{1}{3x^2}$ : $D_x\left[\frac{1}{3x^2}\right] = -\frac{2}{3x^3}$
Derivative of the constant $2$ is $0$ .
Combining these results, we get: $D_x \left[ 4\sqrt{x} + \frac{1}{3x^2} + 2 \right] = \frac{2}{\sqrt{x}} - \frac{2}{3x^3}$

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;