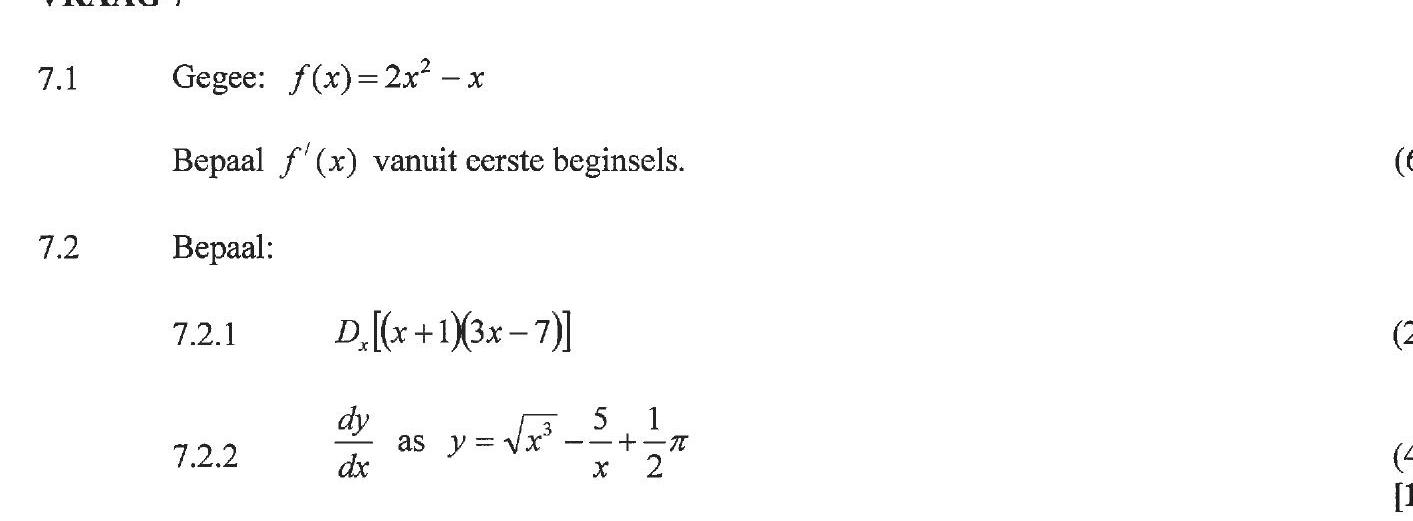Photo AI

Gegee: $f(x) = 2x^2 - x$ Bepaal $f'(x)$ vanuit cerste beginsels - NSC Mathematics - Question 7 - 2017 - Paper 1

Question icon

Question 7

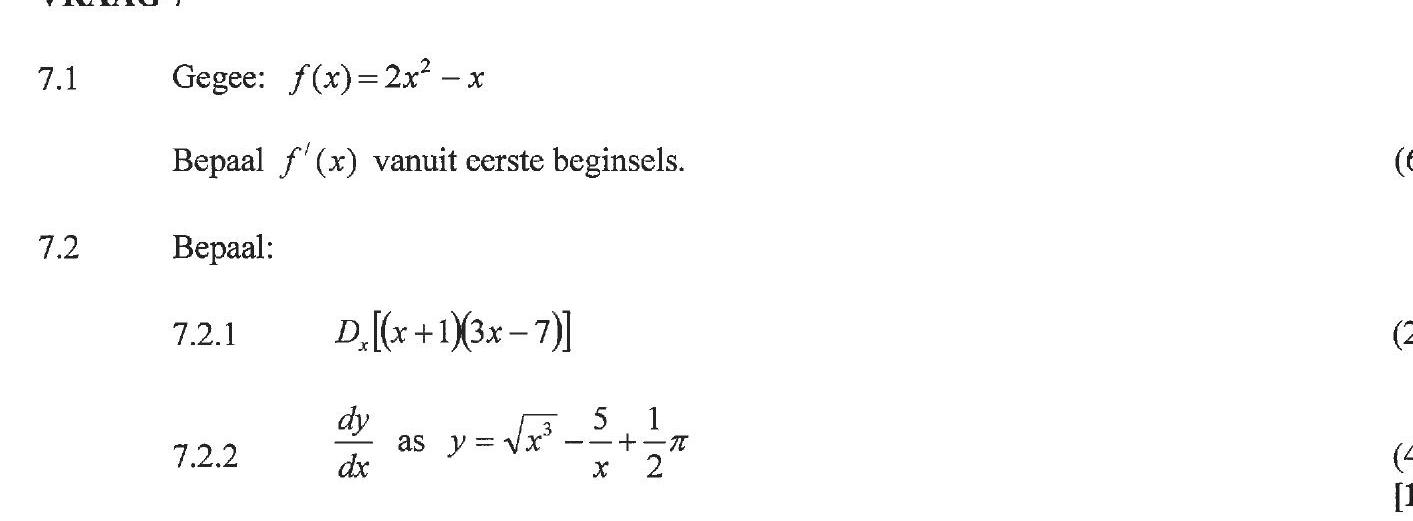
Gegee:-$f(x)-=-2x^2---x$--Bepaal-$f'(x)$-vanuit-cerste-beginsels-NSC Mathematics-Question 7-2017-Paper 1.png

Gegee: $f(x) = 2x^2 - x$ Bepaal $f'(x)$ vanuit cerste beginsels. 7.2 Bepaal: 7.2.1 $D_f[(x+1)(3x-7)]$ 7.2.2 $ rac{dy}{dx}$ as $y = rac{ ext{sqrt}(5 - rac{5}{x}... show full transcript

Worked Solution & Example Answer:Gegee: $f(x) = 2x^2 - x$ Bepaal $f'(x)$ vanuit cerste beginsels - NSC Mathematics - Question 7 - 2017 - Paper 1

Step 1

Bepaal $f'(x)$ vanuit cerste beginsels

96%

114 rated

Answer

To find the derivative of the function f(x)=2x2−xf(x) = 2x^2 - x from first principles, we use the definition of a derivative:

f'(x) = rac{f(x+h) - f(x)}{h} where hh approaches 00.

  1. Calculate f(x+h)f(x+h):

    f(x+h)=2(x+h)2−(x+h)=2(x2+2xh+h2)−x−hf(x+h) = 2(x+h)^2 - (x+h) = 2(x^2 + 2xh + h^2) - x - h

    Simplifying gives:

    f(x+h)=2x2+4xh+2h2−x−hf(x+h) = 2x^2 + 4xh + 2h^2 - x - h

  2. Substitute into the derivative formula:

    f'(x) = rac{(2x^2 + 4xh + 2h^2 - x - h) - (2x^2 - x)}{h}

    Simplifying yields:

    f'(x) = rac{4xh + 2h^2 - h}{h} = 4x + 2h - 1

  3. Taking the limit as hh approaches 00:

    f′(x)=4x−1f'(x) = 4x - 1

Step 2

7.2.1 $D_f[(x+1)(3x-7)]$

99%

104 rated

Answer

To determine the derivative of the function (x+1)(3x−7)(x+1)(3x-7), we first apply the product rule:

The product rule states that if u(x)=(x+1)u(x) = (x+1) and v(x)=(3x−7)v(x) = (3x-7), then:

Df[uv]=u′v+uv′D_f[uv] = u'v + uv'

  1. Find u′u' and v′v':

    u′=1v′=3u' = 1 \\ v' = 3

  2. Substitute and simplify:

    Df[(x+1)(3x−7)]=(1)(3x−7)+(x+1)(3)D_f[(x+1)(3x-7)] = (1)(3x - 7) + (x + 1)(3)

    Distributing gives:

    3x−7+3x+3=6x−43x - 7 + 3x + 3 = 6x - 4

Step 3

7.2.2 $ rac{dy}{dx}$ as $y = rac{ ext{sqrt}(5 - rac{5}{x})}{2 rac{ ext{pi}}{2}}$

96%

101 rated

Answer

To differentiate the function y = rac{ ext{sqrt}(5 - rac{5}{x})}{2 rac{ ext{pi}}{2}}, we start by rewriting it for clarity:

Let k = 2 rac{ ext{pi}}{2}. Therefore, the function can be expressed as:

y = rac{ ext{sqrt}(5 - 5x^{-1})}{k}

  1. Differentiate using the chain rule:

    rac{dy}{dx} = rac{1}{k} rac{1}{2 ext{sqrt}(5 - 5x^{-1})} rac{d}{dx}(5 - 5x^{-1})

  2. Differentiating 5−5x−15 - 5x^{-1}:

    rac{d}{dx}(5 - 5x^{-1}) = 5x^{-2}

  3. Substituting back into our derivative:

    rac{dy}{dx} = rac{5x^{-2}}{2k ext{sqrt}(5 - 5x^{-1})}

This is the final form of the derivative.

Join the NSC students using SimpleStudy...

97% of Students

Report Improved Results

98% of Students

Recommend to friends

100,000+

Students Supported

1 Million+

Questions answered

;