Representing, interpreting and analysing data

Purpose of Graphs

Graphs are used in data handling to:

Explore relationships in data.
Display and report data effectively.
Identify patterns and trends, as well as distributions and relationships. Key features every graph should include:
Clear and fair representation of the findings.
Relationships between variables clearly displayed.
Axes labelled:
- Horizontal (x-axis): Dependent variable.
- Vertical (y-axis): Independent variable.

Types of Graphs

Line graphs
Bar graphs (including compound/stacked bars)
Histograms
Scatter plots
Pie charts
Box and whisker plots

Line Graphs

Used to show relationships between two quantities over time.
Straight lines connect points on a grid to reveal trends.

infoNote

Worked Example:

Scenario: Jabu's TV viewing times (minutes per day) over months.

Month	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov
Time	108	103	108	120	115	122	116	105	110	105	104

Observations:

Trends: TV viewing increases in April, June, and September (likely due to holidays) and decreases during exam months.
Line graphs clearly show trends like increases and decreases, which might not be as obvious in other graph types.

Bar Graphs

Represent data in categories.
The height of each bar reflects the frequency or quantity.
Types of bar graphs:
1. Single bar graph
2. Multiple bar graph
3. Compound/stacked bar graph

infoNote

Worked Example:

Scenario: School tuck shop sales of snacks.

Item	Hot Dogs	Sandwiches	Salads	Burgers
Frequency	15	35	10	12

Solution:

Notes:

Bars can be vertical or horizontal.
Spaces between bars are used for clarity.

infoNote

Worked Example : Household Electronic Usage Survey

1. Scenario

A survey of 1,000 households was conducted in 2001 and 2007 to determine the usage of electronic appliances.

The results were displayed in a bar graph and a table showing the percentage of households using different appliances in both years.

2. Questions & Solutions

a) Percentage Increase in TV Usage (2001 - 2007)?

TV usage in 2001 = 83.3%
TV usage in 2007 = 89.5%
Increase = 89.5% - 83.3% = 6.2% Interpretation: More households adopted TV usage over time.

b) Most Used Appliance in 2001 and 2007?

*In both years, the most used appliance was the radio.
Radio usage in 2001 = 96.8%
Radio usage in 2007 = 93.6% Interpretation: Although radio remained the most common appliance, its usage slightly declined.

c) Appliance That Decreased in Usage from 2001 to 2007?

Radio usage decreased from 96.8% to 93.6%. Interpretation: The decline suggests a shift to newer technologies like TV and DVD players.

d) Number of Households Using Cellphones in 2007?

Cellphone usage in 2007 = 65.0%
Calculation:

65.0\% \times 1000 = 650 \text{ households}

Interpretation: 650 out of 1,000 households used cellphones in 2007.

e) Percentage Difference in Usage (TV vs. DVD Players in 2001)?

TV usage in 2001 = 79.5%
DVD player usage in 2001 = 50.0%
Difference = 79.5% - 50.0% = 29.4% Interpretation: TVs were significantly more common than DVD players in 2001.

Compound Bar Graphs

Compare multiple datasets simultaneously (e.g. different years or groups).
Example: Enrolment of South African children aged 7-13 in primary school (1996 vs 2007).

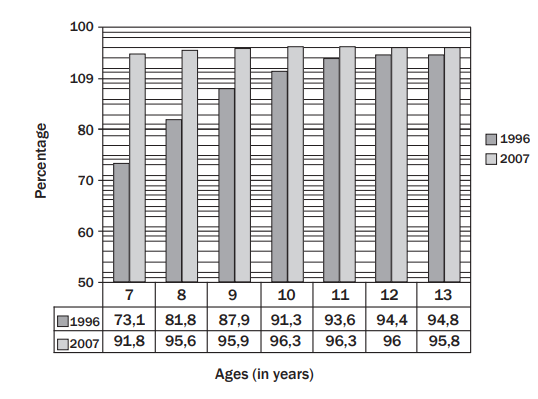
Analysis Example:

Age Group	1996 (%)	2007 (%)
7 years	73.1	81.8
8 years	87.9	97.7
...	...	...

Key Observations:

Increased enrolment in most age groups.
Largest increase was for 8-year-olds.

Histograms

Definition: A histogram is a type of bar graph that shows data grouped into intervals (bins). The height of the bars represents the frequency of data points in each interval.
Key features:
- The bars are adjacent (no gaps between them).
- Used for continuous data.

infoNote

Worked Example:

Scenario: Lengths of school books.

Length (cm)	Frequency
20 – 23.9	4
24 – 26.9	7
27 – 29.9	5
Longer than 30	3

Solution:

Notes:

Histograms effectively show data distribution and patterns.

Activity : Working with Histograms

Mr Smith, an investor from Australia, analyses the salary categories of employees at Raetsiza Company.
Histogram Analysis:
- Horizontal axis: Salary ranges (in thousands of Rands).
- Vertical axis: Number of employees.

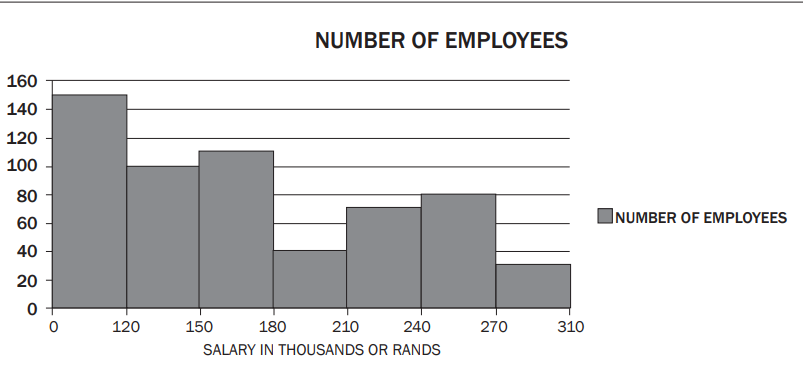
Questions: 4. Total employees? 5. Number of employees earning the lowest salary? 6. Why do fewer employees earn the highest salary? 7. Reasons for fewer employees in the R180 000–R210 000 category. 8. Calculate the new maximum in the R150 000–R180 000 range after a 6% salary increase. Solutions:

Add up the frequencies: $150 + 100 + 110 + 40 + 70 + 80 + 30 = 580$
150 employees earn less than $R120 000$
Fewer employees earn higher salaries due to fewer high-level positions or requirements for special skills.
Senior positions or unique skill requirements.
Increase of $6\%\ \text{of} \ R180000=R190800$

Pie Charts

Definition: A circular graph divided into sectors representing percentages or proportions.
Features:
- Shows relative amounts, not absolute values.
- The percentages in a pie chart must add up to 100%.

infoNote

Worked Example:

The chart below summarises the favourite fruit juice flavours among 120 learners.

Calculation:
$45\% \times 120 = 54$ learners chose fruit cocktail.
$30\% \times 120 = 36$ learners chose apple.
$12.5\% \times 120 = 15$ learners chose grape.
$12.5\% \times 120 = 15$ learners chose litchi.
Advantages of Pie Charts:
Clearly shows proportions at a glance.
Comparison to Bar Graphs:
Bar graphs show specific quantities, while pie charts show percentages.

3. Scatter Plots

Definition: A scatter plot shows the relationship (correlation) between two variables.
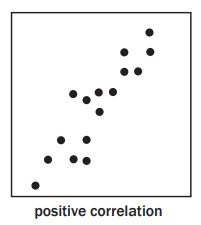
Features:
- Positive correlation: As $x$ increases, $y$ also increases.

Negative correlation: As $x$ increases, $y$ decreases.

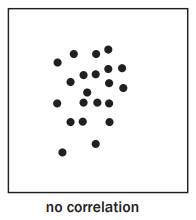
No correlation: Random spread of data.

infoNote

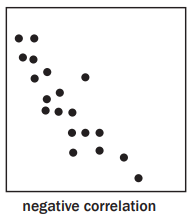
Worked Example:

Plot the relationship between Tourism and Mathematical Literacy marks.

Data for 10 learners is plotted. | TOURISM | 55 | 60 | 20 | 70 | 5 | 40 | 50 | 10 | 30 | 55 | |---|---|---|---|---|---|---|---|---|---|---| | MATHS LIT | 70 | 60 | 40 | 75 | 80 | 30 | 70 | 5 | 45 | 50 |
Observations:
Positive correlation: Higher marks in one subject correlate with higher marks in the other.
Outlier: A learner scored high in one subject and low in the other.

4. Box-and-Whisker Plots

Definition: A box-and-whisker plot graphically represents the five-number summary of a dataset:
- Minimum value
- Lower quartile $(Q_1)$
- Median $(Q_2)$
- Upper quartile $(Q_3)$
- Maximum value
Usage:
- Identify data spread, symmetry, and outliers.

infoNote

Worked Example:

The five-number summary is represented below.

Solution:

Minimum	70
Lower quartile (Q₁)	100
Median (Q₂)	110
Third quartile (Q₃)	115
Maximum value	120

Activity : Box-and-Whisker Plots

The box-and-whisker plot below represents the batting averages of 160 cricketers who have batted in T20 matches since 1 January 2009.

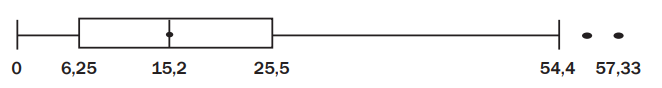
Questions:

What is the name given to the two data points with values 57 and 57.33? Answer: Outliers – data points significantly higher or lower than the rest of the data.
How many players have a batting average less than 6.25? Answer: About 40 players (this is the lower quartile, $Q_1$ , of the data).
What must a batsman's average be for him to be in the top quartile? Answer: Greater than 25.5 (this is the upper quartile, $Q_3$ ).
Jacques Kallis is the South African player with the highest batting average. If his average is 48.4, how does he compare with other batsmen? Answer:

He is in the top quartile.
His score is close to the highest batting averages in the dataset, comparing favourably with the best.

Representing, interpreting and analysing data Simplified Revision Notes for NSC Mathematical Literacy

Representing, interpreting and analysing data

Purpose of Graphs

Types of Graphs

Line Graphs

Worked Example:

Observations:

Bar Graphs

Worked Example:

Notes:

Worked Example : Household Electronic Usage Survey

1. Scenario

2. Questions & Solutions

a) Percentage Increase in TV Usage (2001 - 2007)?

b) Most Used Appliance in 2001 and 2007?

c) Appliance That Decreased in Usage from 2001 to 2007?

d) Number of Households Using Cellphones in 2007?

e) Percentage Difference in Usage (TV vs. DVD Players in 2001)?

Compound Bar Graphs

Analysis Example:

Histograms

Worked Example:

Activity : Working with Histograms

Pie Charts

Worked Example:

3. Scatter Plots

Worked Example:

4. Box-and-Whisker Plots

Worked Example:

Activity : Box-and-Whisker Plots

500K+ Students Use These Powerful Tools to Master Representing, interpreting and analysing data For their NSC Exams.

Other Revision Notes related to Representing, interpreting and analysing data you should explore