Photo AI
Last Updated Sep 27, 2025
Definition of Gradient Simplified Revision Notes for A-Level AQA Maths Pure
Revision notes with simplified explanations to understand Definition of Gradient quickly and effectively.
226+ students studying
7.1.1 Definition of Gradient
The Gradient of
The gradient function of is:
Example 1: Finding the Gradient of when
-
Differentiate the function:
-
Substitute into the differentiated function:
Example 2: Finding the Equation of the Tangent Line to when
- Differentiate the function:
- Evaluate the derivative at :
The point of tangency is:
The equation of the tangent line is:
- Expanding the equation:
Differentiation: Gradient of a Curve
A curve (unless it is a straight line) has different gradients at different points. The gradient of a curve is defined as being the gradient of a tangent to a curve at a given point.
e.g. Estimate using a detailed plot of , its gradient when and
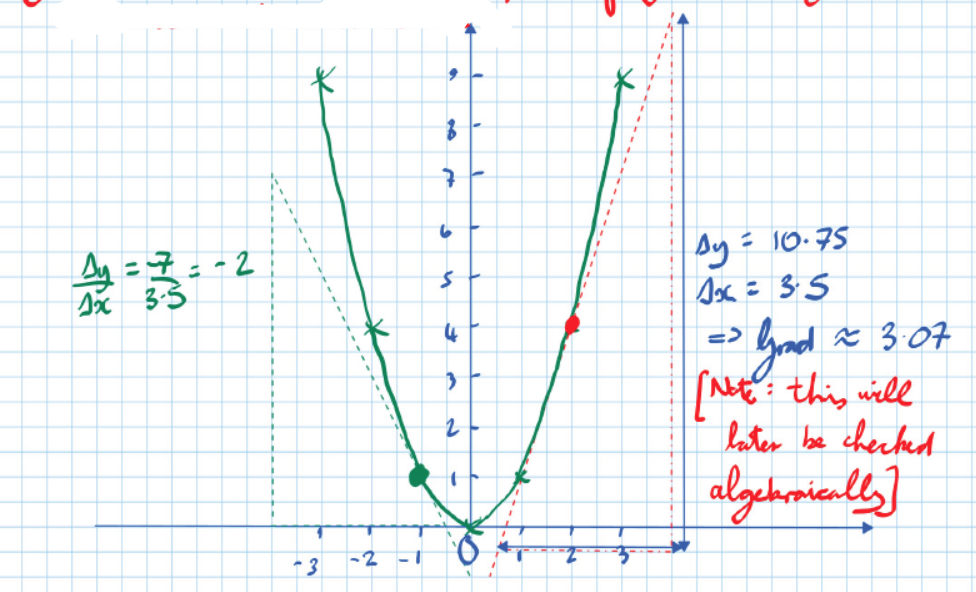
The disadvantage of this method is that it only gives an estimate that depends heavily on the quality of the curve drawn.
An algebraic method exists that allows us to find a formula for the gradient of a curve. We shall restrict all of our examples only to equations involving powers of .
Summary
- The gradient of is .
- When finding the equation of a tangent, differentiate the function, substitute the given -value, and use the point-slope form of a line to find the equation.
500K+ Students Use These Powerful Tools to Master Definition of Gradient For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
40 flashcards
Flashcards on Definition of Gradient
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards4 quizzes
Quizzes on Definition of Gradient
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes42 questions
Exam questions on Definition of Gradient
Boost your confidence with real exam questions.
Try Maths Pure Questions2 exams created
Exam Builder on Definition of Gradient
Create custom exams across topics for better practice!
Try Maths Pure exam builder18 papers
Past Papers on Definition of Gradient
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Definition of Gradient you should explore
Discover More Revision Notes Related to Definition of Gradient to Deepen Your Understanding and Improve Your Mastery
