7.1.2 First Principles Differentiation

The following example shows how to find a formula for the gradient of $y = x^2$ .

infoNote

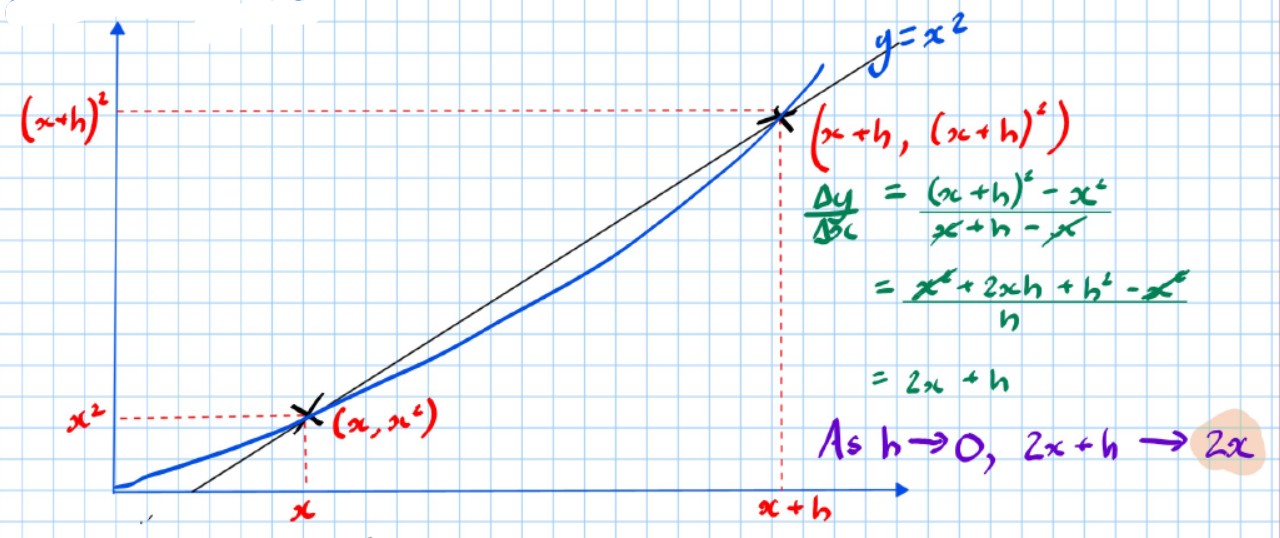
Draw a chord (a rubbish tangent) between two points on the curve.
Label the $x$ coordinates of the points at which the chord intersects the curve as $x$ and $x+h$ . Also, label the corresponding $y$ coordinates.
Algebraically work out the gradient of the chord.
The chord becomes a tangent as $h \to 0$ (" $h$ approaches 0" or " $h$ tends to 0").

infoNote

The gradient of $y = x^2$ is given by the formula $2x$ , i.e., the gradient at any point $(x, y)$ is $2 \times$ the $x$ -coordinate.

Summary: The gradient of $F(x)$ is given by the formula

\lim_{{h \to 0}} \frac{F(x+h) - F(x)}{h}

The limit as $h$ approaches 0.

Gradient of $y = x^4$

$\lim_{{h \to 0}} \frac{(x+h)^4 - x^4}{h} = \lim_{{h \to 0}} \frac{x^4 + 4x^3h + 6x^2h^2 + 4xh^3 + h^4 - x^4}{h}$

$= \lim_{{h \to 0}} (4x^3 + 6x^2h + 4xh^2 + h^3) = :highlight[4x^3]$

(Table showing the relationship between $F(x)$ and its gradient for different powers of $x$ )

$F(x) = x^1$ , Gradient = $1x^0$
$F(x) = x^2$ , Gradient = $2x^1$
$F(x) = x^3$ , Gradient = $3x^2$
$F(x) = x^4$ , Gradient = $4x^3$ $F(x) = x^n, \text{ Gradient } = :highlight[nx^{n-1}]$

The gradient function for $x^n$ , $n \in \mathbb{R}$ is given by $nx^{n-1}$ .

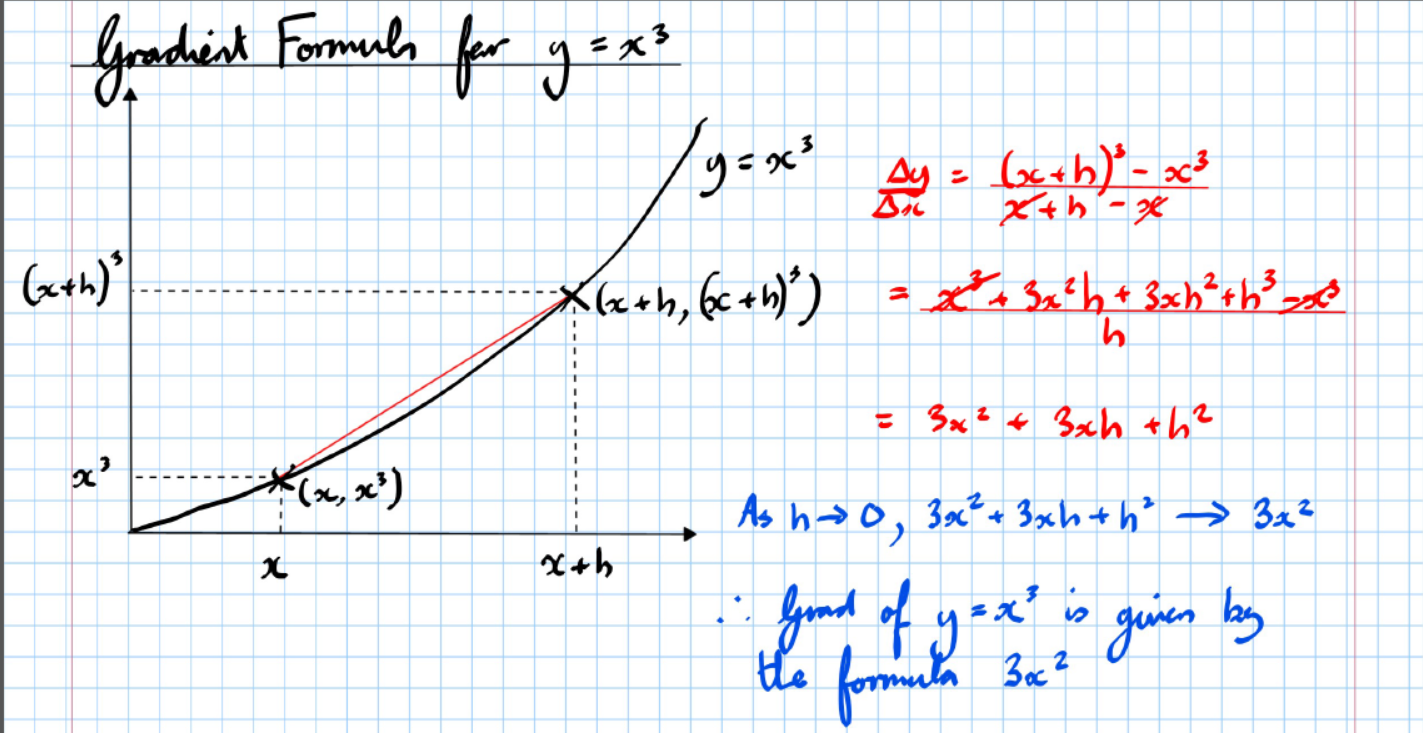
Further Differentiation by First Principles

infoNote

Example: Differentiate $x^2 + 2x$ by first principles. Find the gradient formula:

\lim_{h \to 0} \left (\frac{f(x+h) - f(x)}{h}\right ) = \lim_{h \to 0} \left (\frac{(x+h)^2 + 2(x+h) - (x^2 + 2x)}{h} \right)

= \lim_{h \to 0} \left (\frac{\cancel {x^2} + 2xh + h^2 \cancel {+ 2x} + 2h - \cancel {x^2} - \cancel {2x}}{h} \right)

= \lim_{h \to 0} \left (\frac{2xh + h^2 + 2h}{h}\right )

= \lim_{h \to 0} (2x + h + 2)

= :highlight[2x + 2] \quad \left(= \frac{dy}{dx} \text{ or } f'(x)\right) \quad

The technical names for the gradient formula is:

infoNote

The differential can be denoted in two main ways:

$\dfrac{dy}{dx}$ , which is pronounced " $dy$ by $dx$ ". This means the limit as $h \to 0$ of the gradient of the chord.
$f'(x)$ , where the number of dashes indicates how many times the function has been differentiated.

infoNote

Example: If $y = 3x^2 + 2x$ , use first principles to find $\dfrac{dy}{dx}$ .

\dfrac{dy}{dx} = \lim_{h \to 0} \left (\frac{f(x+h) - f(x)}{h} \right)

= \lim_{h \to 0} \left (\frac{3(x+h)^2 + 2(x+h) - (3x^2 + 2x)}{h} \right)

= \lim_{h \to 0} \left (\frac{3(x^2 + 2xh + h^2) + 2x + 2h - 3x^2 - 2x}{h}\right)

= \lim_{h \to 0} \left (\frac{\cancel {3x^2} + 6xh + 3h^2 + \cancel {2x} + 2h - \cancel {3x^2} - \cancel {2x}}{h}\right)

= \lim_{h \to 0} \left ((6x + 3h + 2)\right ) = :highlight[6x + 2]

\Rightarrow \text{When } x = 1, \dfrac{dy}{dx} = 6(1) + 2 = :success[8]