11.1.3 Rotational Motion

Key Terms and Definitions

1. Angular Displacement ($θ$): The angle an object turns through in any given direction, measured in radians (rad).
2. Angular Speed ($ω$): The rate at which an object rotates, defined as the angle it covers per unit of time. Units are rads⁻¹.
3. Angular Velocity ($ω$): The rate of change of angular displacement per unit of time, with a direction (can be clockwise or anti-clockwise). Units are rads⁻¹.
4. Angular Acceleration ($α$): The rate of change of angular velocity over time, measured in rads⁻²

Relationship between Linear and Rotational Quantities

Rotational quantities have analogous equations to those in linear motion, making it easier to understand and remember rotational motion equations.

Linear Quantity	Rotational Quantity
Linear Velocity $v = \frac{\text{displacement}}{\text{time}}$	Angular Velocity $\omega = \frac{\Delta \theta}{\Delta t}$
Linear Acceleration $a = \frac{\text{velocity}}{\text{time}}$	Angular Acceleration $\alpha = \frac{\Delta \omega}{\Delta t}$

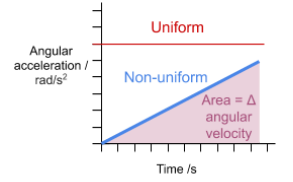
Uniform and Non-Uniform Angular Acceleration

• Uniform Angular Acceleration: This occurs when angular acceleration remains constant over time.
  • In this case, a graph of angular velocity against time will be a straight line.
  • The gradient of the line on this graph gives the angular acceleration.
  • The area under this graph represents angular displacement.
• Non-Uniform Angular Acceleration: When angular acceleration varies with time.
  • The angular velocity graph will not be a straight line, but curved.
  • To find acceleration at a specific point, draw a tangent and calculate its gradient.

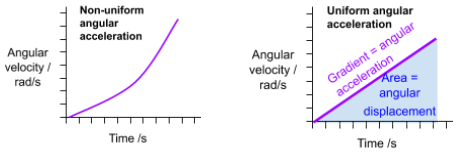
Graphs Related to Uniform Angular Acceleration

1. Angular Velocity vs. Time:

• For uniform acceleration, this graph is a straight line.
• Gradient of the line = Angular acceleration.
• Area under the line = Angular displacement.

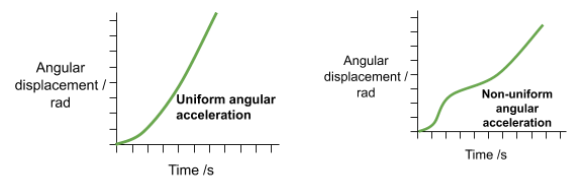
2. Angular Displacement vs. Time:

• For uniform acceleration, angular displacement increases quadratically with time, creating a parabolic curve.

Equations of Motion for Uniform Angular Acceleration

These equations are similar to the SUVAT equations for linear motion but applied to rotational variables:

Linear Motion Equation	Rotational Motion Equation
$v = u + at$	$\omega_2 = \omega_1 + \alpha t$
$s = \frac{1}{2} (u + v)t$	$\theta = \frac{1}{2} (\omega_1 + \omega_2)t$
$s = ut + \frac{1}{2}at^2$	$\theta = \omega_1 t + \frac{1}{2} \alpha t^2$
$v^2 = u^2 + 2as$	$\omega_2^2 = \omega_1^2 + 2 \alpha \theta$

Where:

• $\theta$ = Angular displacement
• $\omega_1$ = Initial angular velocity
• $\omega_2$ = Final angular velocity
• $\alpha$ = Angular acceleration
• $t$ = Time