Photo AI
Last Updated Sep 27, 2025
Torque and angular acceleration Simplified Revision Notes for A-Level AQA Physics
Revision notes with simplified explanations to understand Torque and angular acceleration quickly and effectively.
419+ students studying
11.1.4 Torque and angular acceleration
Torque
Torque is the product of a force and its distance from the axis of rotation . Torque is responsible for causing rotation and is measured in newton-metres ().
The equation for torque is:
Where:
- = Torque
- = Force applied
- = Distance from the axis of rotation
Explanation of Torque
The concept of torque can be visualised with a wheel and axle setup:
- When a mass is attached to the axle, it exerts a force at a distance from the centre. This force generates torque, leading to angular acceleration in the wheel.
Increasing Angular Acceleration
The angular acceleration of an object can be increased by:
- Increasing the mass (), which increases the torque.
- Using a lighter wheel, reducing the moment of inertia, making it easier to accelerate.
Torque, Inertia, and Angular Acceleration Relationship
The relationship between torque , moment of inertia ($$ I ), and angular acceleration is given by:
Where:
- = Torque
- = Moment of inertia, a measure of how much an object resists rotational acceleration
- = Angular acceleration
This equation is analogous to Newton's second law for linear motion, where force results in acceleration. Here, torque results in angular acceleration.
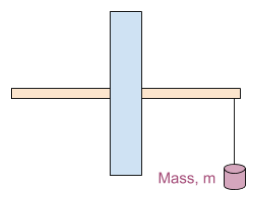
Worked Example
Consider a mass attached to the end of a horizontal rod, free to rotate about a vertical axis:
- Calculate Torque: Given a force applied at a distance from the axis, calculate .
- Determine Angular Acceleration: With the moment of inertia known, use to find the angular acceleration
500K+ Students Use These Powerful Tools to Master Torque and angular acceleration For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
60 flashcards
Flashcards on Torque and angular acceleration
Revise key concepts with interactive flashcards.
Try Physics Flashcards6 quizzes
Quizzes on Torque and angular acceleration
Test your knowledge with fun and engaging quizzes.
Try Physics Quizzes29 questions
Exam questions on Torque and angular acceleration
Boost your confidence with real exam questions.
Try Physics Questions27 exams created
Exam Builder on Torque and angular acceleration
Create custom exams across topics for better practice!
Try Physics exam builder56 papers
Past Papers on Torque and angular acceleration
Practice past papers to reinforce exam experience.
Try Physics Past PapersOther Revision Notes related to Torque and angular acceleration you should explore
Discover More Revision Notes Related to Torque and angular acceleration to Deepen Your Understanding and Improve Your Mastery
