Photo AI
Last Updated Sep 27, 2025
Motion along a straight line Simplified Revision Notes for A-Level AQA Physics
Revision notes with simplified explanations to understand Motion along a straight line quickly and effectively.
234+ students studying
4.1.3 Motion along a straight line
- Speed: A scalar quantity that describes how fast an object is moving, without any regard for direction.
- Displacement (): A vector quantity representing the overall distance moved from the initial position, including direction.
- Velocity (): The rate of change of displacement with respect to time, given by:
- Acceleration (): The rate of change of velocity with respect to time, given by:
Types of Velocity
- Instantaneous Velocity: The velocity at a specific moment in time. It can be found by determining the gradient of a tangent line on a displacement-time graph.
- Average Velocity: The velocity over a specified time period. It is calculated by dividing the total displacement by the total time taken.
Uniform Acceleration
When an object experiences constant acceleration, we describe it as having uniform acceleration.
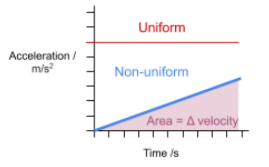
Interpreting Motion Graphs
- Acceleration-Time Graphs:
- Show how velocity changes over time.
- The area under the graph gives the change in velocity.
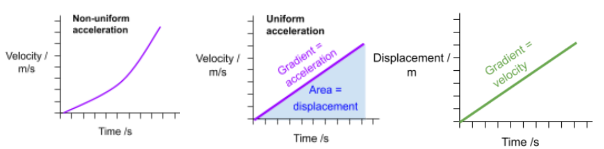
- Velocity-Time Graphs:
- Show how velocity varies over time.
- The gradient of this graph represents acceleration.
- The area under the graph represents displacement.
- Displacement-Time Graphs:
- Show the change in displacement over time.
- The gradient of this graph represents velocity.
Equations of Motion for Uniform Acceleration
For objects moving with uniform acceleration, the following equations of motion apply:
Where:
- = displacement
- = initial velocity
- = final velocity
- = acceleration
- = time Tip: When solving problems, list out known and unknown values and choose the equation that best fits.
Worked Example Problem: A stone is dropped from a bridge that is m above the water. Calculate:
- The final velocity of the stone just before it hits the water.
- The time it takes to reach the water. Solution:
- List known values:
- (since it's dropped)
- (acceleration due to gravity)
- Calculate Final Velocity: Using the equation :
- Calculate Time: Using the equation :
Key Points
- Speed and Velocity: Speed is scalar, while velocity is a vector.
- Acceleration: Represents change in velocity over time.
- Uniform Acceleration Equations: Use these equations to solve motion problems with constant acceleration.
- Graph Analysis: Displacement-time, velocity-time, and acceleration-time graphs each provide unique insights into motion.
500K+ Students Use These Powerful Tools to Master Motion along a straight line For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
80 flashcards
Flashcards on Motion along a straight line
Revise key concepts with interactive flashcards.
Try Physics Flashcards8 quizzes
Quizzes on Motion along a straight line
Test your knowledge with fun and engaging quizzes.
Try Physics Quizzes29 questions
Exam questions on Motion along a straight line
Boost your confidence with real exam questions.
Try Physics Questions27 exams created
Exam Builder on Motion along a straight line
Create custom exams across topics for better practice!
Try Physics exam builder56 papers
Past Papers on Motion along a straight line
Practice past papers to reinforce exam experience.
Try Physics Past PapersOther Revision Notes related to Motion along a straight line you should explore
Discover More Revision Notes Related to Motion along a straight line to Deepen Your Understanding and Improve Your Mastery
