8.1.5 Nuclear Radius

Understanding Nuclear Radius

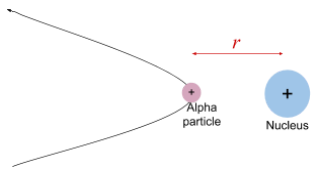
The nuclear radius of an atom can be estimated by calculating the distance of closest approach of a charged particle, such as an alpha particle, fired at a gold nucleus.

Distance of Closest Approach:

• As the alpha particle moves towards the positively charged nucleus, it experiences a repulsive electrostatic force.
• The particle's kinetic energy is converted into electric potential energy as it slows down.
• The point at which the alpha particle stops and has zero kinetic energy marks the distance of closest approach, symbolised as $r$.
• The electric potential $V$ at this point is given by:

$$V = \frac{1}{4 \pi \epsilon_0} \frac{Q}{r}$$

Where:

• $\epsilon_0$ is the permittivity of free space,
• $Q$ is the charge of the nucleus,
• $r$ is the distance of closest approach.

Electric Potential Energy Calculation:

• Electric potential energy $E_{\text{elec}}$ at this distance can be calculated as:

$$E_{\text{elec}} = \frac{1}{4 \pi \epsilon_0} \frac{Q_1 Q_2}{r}$$

• This energy represents the work done to bring the charges to this distance apart.

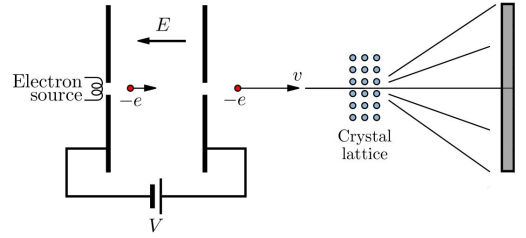
Electron Diffraction as an Alternative Method:

• Electron diffraction offers a more accurate measure of nuclear radius as it avoids interaction with the strong nuclear force.
• Electrons, being leptons, do not experience this force, unlike alpha particles, providing a clearer measure.
• High-speed electrons with a De Broglie wavelength around 10^-15 m pass through a thin material, creating a diffraction pattern.

Diffraction Pattern Analysis:

• The pattern observed is a series of concentric circles.
• The intensity of these circles diminishes as distance from the centre increases.
• By plotting a graph of intensity against diffraction angle, we can measure the diffraction angle of the first minimum to estimate nuclear radius using:

$$\sin \theta = \frac{0.61 \lambda}{R}$$

Where:

• $\theta$ is the diffraction angle,
• $\lambda$ is the electron's De Broglie wavelength,
• $R$ is the nuclear radius.

Graphical Method for Nuclear Radius:

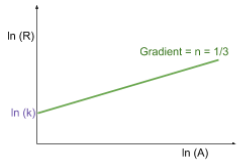
• A logarithmic plot of nuclear radius $R$ against nucleon number $A$ (mass number) provides further insight:

$$R = kA^{1/3}$$

• Taking logs, we get:

$$\ln R = \ln k + \frac{1}{3} \ln A$$

• Plotting $\ln \ R$ against $\ln A$, the gradient of this line (approximately 1/3) and the intercept $\ln k$ help determine the relationship.

Nuclear Density:

• Using the above relationship, it can be shown that nuclear density is constant across all nuclei.
• Calculation shows nuclear density around 1.45 × 10^17 kg/m³, which indicates that most of an atom's mass is concentrated in the nucleus, with the rest being mostly empty space.