Photo AI
Last Updated Sep 27, 2025
Simple Harmonic Motion Simplified Revision Notes for A-Level AQA Physics
Revision notes with simplified explanations to understand Simple Harmonic Motion quickly and effectively.
372+ students studying
Simple Harmonic Motion
Part 1: Mass-Spring System
Equipment
- Spring: The oscillating element.
- 50g masses with holder: Allows for mass adjustment up to 500g.
- Stand and clamp: To securely hold the spring.
- Pin and Blu-Tack: Used as a fiducial marker at the equilibrium position.
- Metre ruler: For accurate positioning.
- Stopwatch: To time oscillations.
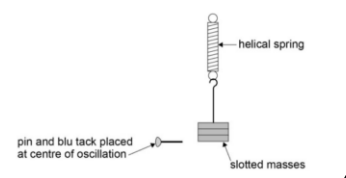
Method
- Setup:
- Assemble the apparatus as shown, with the spring attached to the stand and a mass holder at the bottom. Place the fiducial marker at the system's equilibrium position.
- Start Oscillations:
- Displace the mass holder vertically downwards by a small distance and release. The system will oscillate vertically.
- Measure Oscillation Time:
- Start timing as the mass passes the fiducial marker. Measure the time for 10 oscillations and record it as T₁₀.
- Calculate the time period T for one oscillation by dividing T₁₀ by 10.
- Increase Mass:
- Add a 50g mass, and repeat the timing procedure. Record the time period T for each total mass up to 500g.
- Repeat for Accuracy:
- Perform each measurement at least twice more to ensure accuracy.
Graphs and Calculations
- Graph of T² vs. m:
- Plot T² (y-axis) against mass m (x-axis). Draw a line of best fit.
- The gradient of this graph is 4π²/k, where k is the spring constant.
- Equation of Motion:
- The period of a mass-spring system in SHM is given by:
- Using the gradient of the graph, calculate k for the spring.
Safety
- Falling Masses: Be careful with suspended masses to prevent injury if they fall. Avoid pulling the spring too far downwards.
Improvements and Notes
- Vertical Oscillation: Ensure the spring oscillates vertically; any horizontal motion can affect timing accuracy.
- Use of Fiducial Marker: The marker should be placed at the centre of oscillation to reduce timing errors.
- Data Logger: Using a motion tracker or data logger can improve timing accuracy by removing human reaction time errors.
Part 2: Simple Pendulum
Equipment
- Pendulum bob on 2m string: For generating oscillations.
- Stand and clamp: To secure the pendulum.
- Pin and Blu-Tack: Fiducial marker at equilibrium position.
- Metre ruler: To measure string length.
- Stopwatch: To time oscillations.
- Two wooden blocks: To support the pendulum setup.
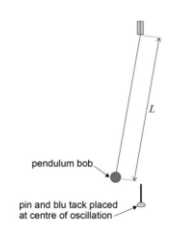
Method
- Setup:
- Set up the pendulum with a string length L of 1.5m (distance from the suspension point to the bob's centre of mass). Place the fiducial marker at the equilibrium position.
- Initiate Oscillations:
- Displace the pendulum by a small angle (less than 15°) and release. Ensure the motion is in a straight line.
- Measure Oscillation Time:
- Start timing when the bob passes the fiducial marker. Measure the time for 10 oscillations and record as T₁₀.
- Calculate the period T for one oscillation by dividing T₁₀ by 10.
- Decrease Length:
- Shorten L by 0.100m increments, measuring T for each length down to 0.500m.
- Repeat for Accuracy:
- Repeat each measurement twice more to obtain mean values.
Graphs and Calculations
- Graph of T² vs. L:
- Plot T² (y-axis) against pendulum length L (x-axis) and draw a line of best fit.
- The gradient of this graph is 4π²/g, where g is the acceleration due to gravity.
- Equation of Motion:
- The period of a pendulum in SHM is:
- Calculate g from the gradient.
Safety
- Low Risk: There are minimal safety concerns, but ensure the pendulum has enough space to swing without obstruction.
Improvements and Notes
- Small Bob: Use a small pendulum bob to make length measurements easier.
- Length Accuracy: Measure from the centre of mass of the bob for accurate L.
- Data Logging: As with the mass-spring system, a motion tracker can improve timing accuracy by eliminating manual timing errors.
Key Concepts
- Simple Harmonic Motion (SHM): Both systems exhibit SHM, characterised by a restoring force proportional to displacement.
- Graphical Analysis: For both systems, plotting T² against mass (for spring) or length (for pendulum) provides a way to calculate spring constants and gravitational acceleration.
- Equation Derivations: Understanding the derivations of T in both systems reinforces the mathematics behind oscillatory motion in physics.
500K+ Students Use These Powerful Tools to Master Simple Harmonic Motion For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
130 flashcards
Flashcards on Simple Harmonic Motion
Revise key concepts with interactive flashcards.
Try Physics Flashcards13 quizzes
Quizzes on Simple Harmonic Motion
Test your knowledge with fun and engaging quizzes.
Try Physics Quizzes29 questions
Exam questions on Simple Harmonic Motion
Boost your confidence with real exam questions.
Try Physics Questions27 exams created
Exam Builder on Simple Harmonic Motion
Create custom exams across topics for better practice!
Try Physics exam builder56 papers
Past Papers on Simple Harmonic Motion
Practice past papers to reinforce exam experience.
Try Physics Past PapersOther Revision Notes related to Simple Harmonic Motion you should explore
Discover More Revision Notes Related to Simple Harmonic Motion to Deepen Your Understanding and Improve Your Mastery
