1.1.6 Regions in Argand Diagrams

Overview

You also need to know how to represent regions on the Argand diagram.

A region represents a set of complex numbers that satisfy a particular condition, and these regions can take various shapes such as circles, half-planes, and areas between curves.

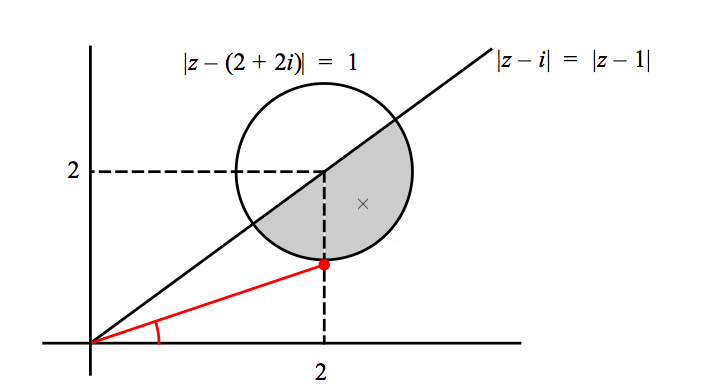
Shading Regions Based on Modulus

The modulus of a complex number gives its distance from the origin or another point on the Argand diagram. We can define regions by using inequalities involving the modulus.

Inequality of the form $|z - z_1| < r$

• This represents the set of points inside a circle with centre at $z_1$ and radius $r$
• The boundary of the circle, where $|z - z_1| = r$, is not included in the region.

Inequality of the form $|z - z_1| > r$

• This represents the set of points outside a circle with centre at $z_1$ and radius $r$.
• The points outside the circle, but not on its boundary, are included in the region.

Shading Regions Based on Argument

The argument of a complex number gives the angle that the line joining the point to the origin makes with the positive real axis. We can define regions using inequalities involving the argument.

Inequality of the form $\alpha < \arg(z - z_1) < \beta$

• This represents a sector between two rays (lines starting from $z_1$ at angles $\alpha$ and $\beta$).
• The region includes all points whose arguments fall between the two specified angles.

Combining Modulus and Argument Conditions

We can combine conditions on the modulus and argument to define more specific regions.

Worked Example:

---